The decision whether to buy a financial asset and add it to an existing portfolio depends on three main variables: (1) what is the asset’s return? (2) What is the asset’s level of risk? and (3) how well does the asset fit into my existing portfolio?
The third question is usually answered by looking at the correlation between assets. At the center of this correlation analysis lies the question whether correlations are constant or whether they change over time. For instance, if correlations are time-varying, portfolios need to be rebalanced frequently, risk levels change constantly, and hedging strategies need to be updated continually. Whether investors view asset correlations as constant or time-varying therefore has a large impact on the way they manage financial portfolios.
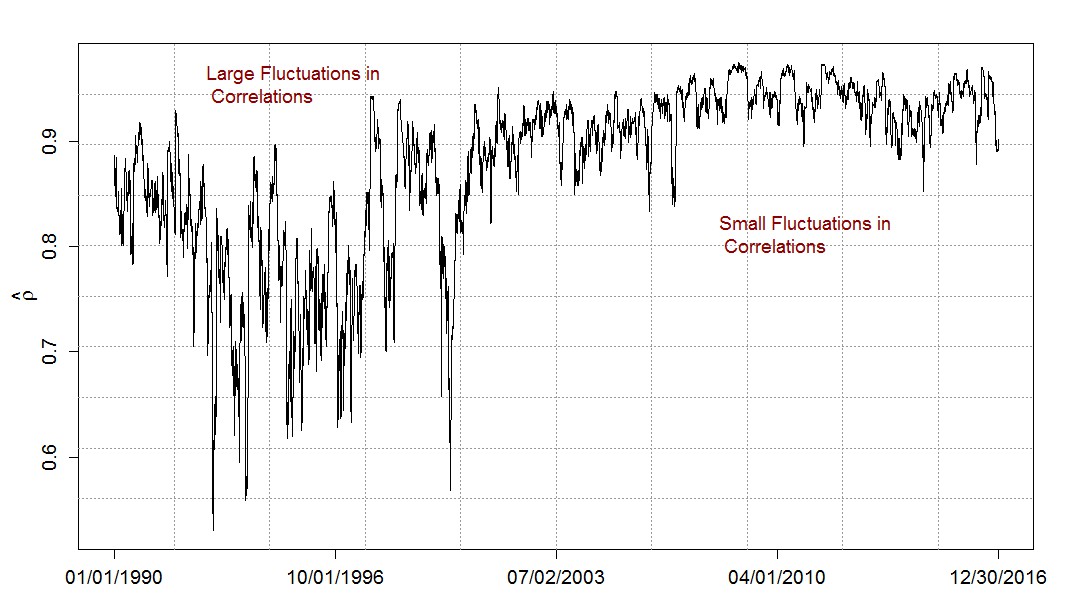
Although correlation is a fundamental and straightforward concept, it cannot be observed in the data and needs to be estimated. The current practice is to treat correlations as time-varying and most empirical results seem to confirm this view. For instance, Figure 1 shows the conditional correlations between the daily returns of the S&P 500 and the NASDAQ index from 1990 to 2016.
Figure 1: Daily time-varying correlations as estimated by popular models (click to enlarge)
Two characteristics that are typical for time-varying correlations stand out. First, correlations undergo large swings over a short period of time. In the 1990’s, correlations frequently moved within a wide range between 0.52 in July 1993 and 0.94 in November 1997. In the literature, this observation has been sometimes interpreted as evidence that the underlying correlation structure is a highly volatile process. Second, the fluctuation in conditional correlations often changes over time. In Figure 1, correlations are highly volatile during the 1990’s but enter a more tranquil period in 2000. During this time, the daily volatility of correlations dropped approximately by half.
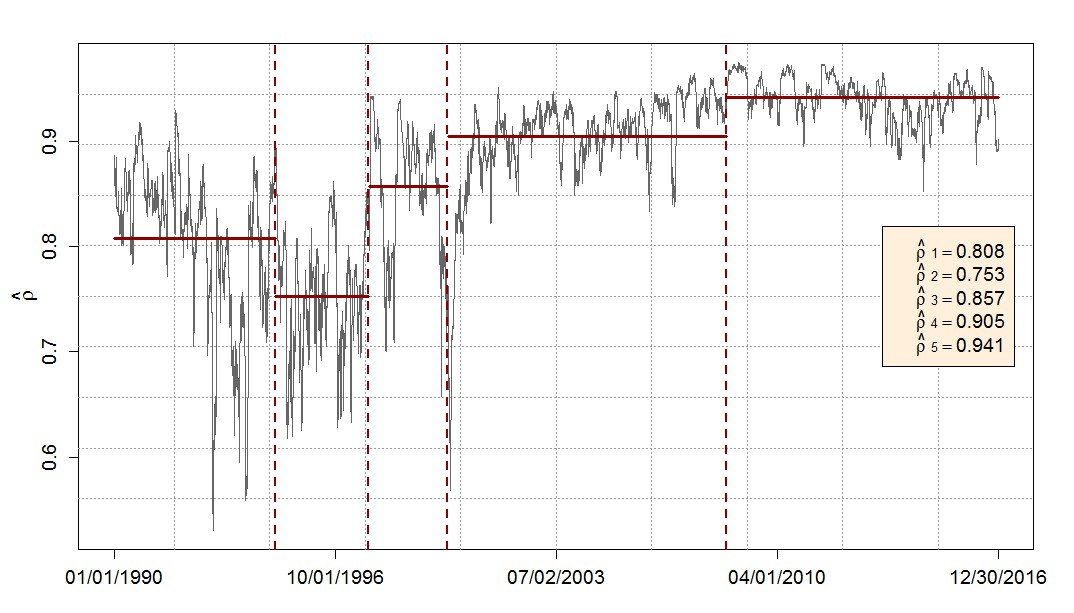
The contribution of our paper is to demonstrate that the correlation estimates generated by models that are routinely used in practice are probably misleading. The large fluctuations during the 1990’s and the small fluctuations during the 2000’s have no fundamental economic cause but are purely artificial results generated by these types of models. We believe that correlations are generally constant but that infrequent economic disruptions can shift the level of correlations. We think that the actual correlation between the S&P 500 and NASDAQ returns probably look more like in Figure 2:
Figure 2: Daily correlations are probably constant
Over time, a number of events have shifted the level of correlations. The breaks shown in Figure 2 correspond to the Mexican peso crisis in 1994, the Asian Crisis in 1997, the burst of the Dot-com bubble which had its climax in March 2000, and the default of Lehman Brothers in September 2008. Between the breaks, however, correlations do not change.
If correlations are actually constant, one question is why time-varying models have become so popular. Why do many academics and practitioners believe that correlations fluctuate widely from day to day? The popularity of these models can be explained by the fact that time-varying correlations appear to fit well to the data. The design of these models is an extension of volatility models for individual assets to a portfolio of multiple assets. Given the success of volatility models in finance, the multivariate extension to correlations seems straightforward. The fact that the correlation parameters that are estimated in the process are often statistically significant seems to confirm this step. However, we argue that correlations are quite different in nature. While important economic and financial news such as economic activity, interest rate changes, and oil prices affect the volatility of financial assets, the relevance and impact of this news is often similar across firms. As a consequence, volatility is constantly exposed to news and therefore time-varying but correlations are not.
Recent studies have started to adopt the constant correlation view and have proposed models that accommodate constant correlations with infrequent level changes (see for instance Aslanidis and Martinez, 2016). The perception therefore seems to change slowly in favor of that view. It is time that we rethink our understanding of correlations as an indicator of comovement in financial assets.
♣♣♣
Notes:
- This blog post is based on the authors’ paper Are Correlations Constant? Empirical and Theoretical Results on Popular Correlation Models in Finance, University of St.Gallen, School of Finance Research Paper No. 2016/13
- The post gives the views of its author, not the position of LSE Business Review or the London School of Economics.
- Featured image credit:
- Before commenting, please read our Comment Policy
 Zeno Adams is an Assistant Professor of Finance at the University of St.Gallen, Switzerland. His main research interests are empirical topics in commodity markets and real estate finance.
Zeno Adams is an Assistant Professor of Finance at the University of St.Gallen, Switzerland. His main research interests are empirical topics in commodity markets and real estate finance.
 Thorsten Glück is with Frankfurt based consultancy d-fine GmbH. His consulting activity focuses strongly on quantitative modeling of commodity derivatives. He studied economics and econometrics at the University of Freiburg and European Business School and takes currently part at the MSc. Program in Mathematical Finance at the University of Oxford.
Thorsten Glück is with Frankfurt based consultancy d-fine GmbH. His consulting activity focuses strongly on quantitative modeling of commodity derivatives. He studied economics and econometrics at the University of Freiburg and European Business School and takes currently part at the MSc. Program in Mathematical Finance at the University of Oxford.
 Roland Füss is Full Professor of Finance at the University of St.Gallen and Member of the Board of the Swiss Institute of Banking and Finance (s/bf-HSG) and the School of Finance. He is also a research associate at the Centre for European Economic Research (ZEW), Mannheim, Germany. Prof. Füss is a member of the editorial board of several academic journals. His main research topics are in the field of empirical asset pricing, portfolio optimization, real estate finance and economics, risk management, and applied financial econometrics. Prof. Füss has authored numerous articles in economics, finance, and real estate journals such as Journal of Financial and Quantitative Analysis, Review of Finance, Journal of Money, Credit and Banking, Journal of Banking and Finance, Public Choice, and Real Estate Economics.
Roland Füss is Full Professor of Finance at the University of St.Gallen and Member of the Board of the Swiss Institute of Banking and Finance (s/bf-HSG) and the School of Finance. He is also a research associate at the Centre for European Economic Research (ZEW), Mannheim, Germany. Prof. Füss is a member of the editorial board of several academic journals. His main research topics are in the field of empirical asset pricing, portfolio optimization, real estate finance and economics, risk management, and applied financial econometrics. Prof. Füss has authored numerous articles in economics, finance, and real estate journals such as Journal of Financial and Quantitative Analysis, Review of Finance, Journal of Money, Credit and Banking, Journal of Banking and Finance, Public Choice, and Real Estate Economics.