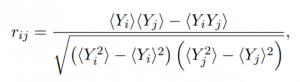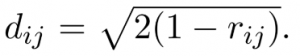Raymond Pang is a PhD student who joined the Department of Mathematics in September 2018. His research interests are in systemic risk and financial networks, relating to the mathematical modelling of events such as the 2008 financial crisis.
Raymond Pang is a PhD student who joined the Department of Mathematics in September 2018. His research interests are in systemic risk and financial networks, relating to the mathematical modelling of events such as the 2008 financial crisis.
In this blog post, Raymond discusses a project he has been working on in the last few months, which tries to understand the impact of COVID-19 on the financial markets.
Before March, I didn’t really have much of an understanding in epidemiology and the mathematical models used to model such processes. But when the lockdown began, I started to read more of the literature and became interested in the uses of network theory within the area. In late March, I received an email about a Net-COVID workshop online series and thought this would be a great chance to learn more, through the given lectures and tutorials.
Within the workshop, there was an opportunity to collaborate with others on a COVID-19 related project using network science. I didn’t know much about epidemiology, but I had an understanding in financial mathematics and proposed a project investigating the impact of COVID-19 on sovereign bond yields. The project generated interest from various people, and we decided to focus on a network-based approach in understanding European sovereign bonds.
In basic terms, a bond is an “I owe you”, where the issuer promises to pay back the investor in timely payments until the date of maturity e.g. 1 year, 10 years or 50 years. In our case, we use sovereign bonds which are bonds issued by national governments. These bonds are particularly interesting to analyse, as this represents a key instrument in supporting the expenditure of national governments which is issued by many countries.
We consider a methodology, the same as in Mantegna (1999) in order to construct a network from historic correlations. For N sovereign bonds, we define Y(i) and Y(j) to be the list of bond yields for i,j. The Pearson correlation r is then used to calculate the correlation between two sovereign bond yields with <,> denoting the average of yield values.
This results in a correlation matrix of dimension NxN, which is symmetric with values of 1 on the diagonal. From the correlation matrix, we can then define the notion of distance d which will represent the link weights of the network between i and j sovereign bonds.
From the distance matrix d, we generate a complete network with N(N-1)/2 pairwise links between N sovereign bonds, which can result in a large network for large N. For economic reasons, we may only be interested in certain aspects of the network and would therefore like to consider a subset of links. A well-known approach is the minimum spanning tree (Kruskal, 1956), where you construct a connected and undirected network by considering the smallest n-1 link weights from d. In terms of the correlations r, this means you prioritise positive correlations within the network structure.
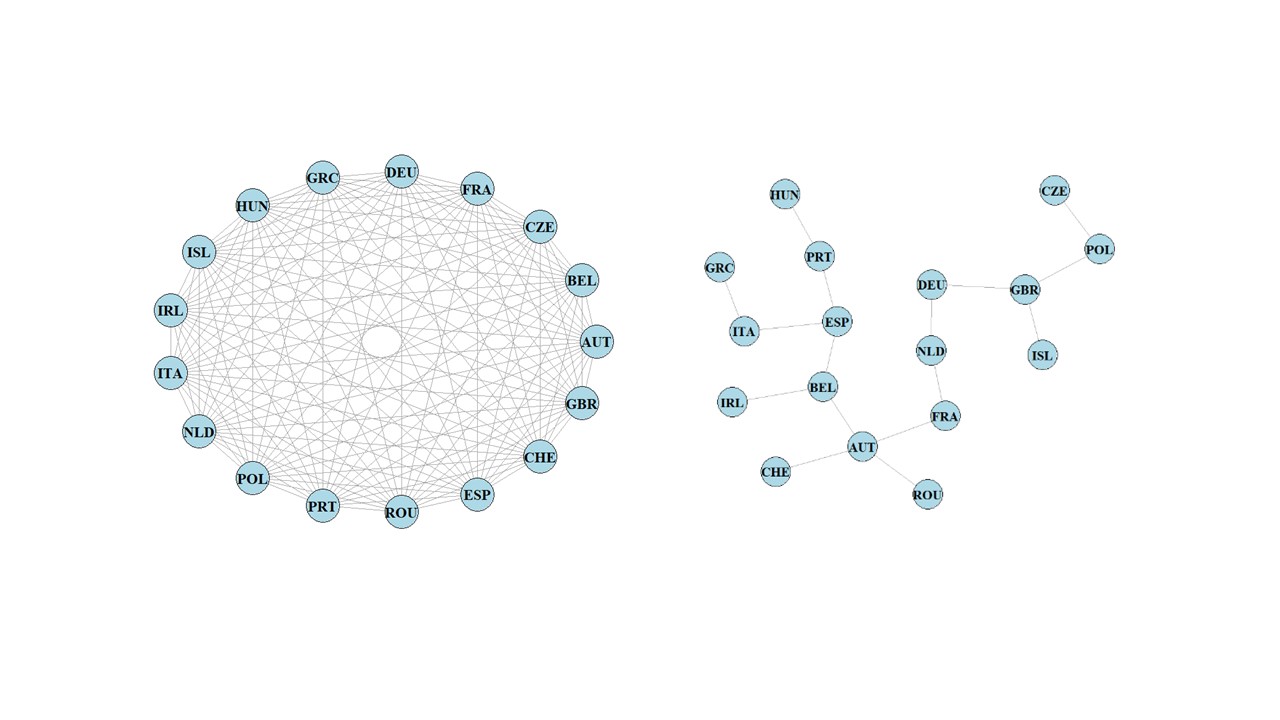
The left figure represents the complete network d for N=17 different European sovereign bonds between the months of January to June 2020, and the right figure represents the minimum spanning tree network. By considering a filtered network, we can identify features of interest from the complete network d and the temporal changes to the network structure over time. When considering the correlations for sovereign bond yields within the COVID-19 period, we show the impact on the mean correlations between sovereign bond yields, but also the preservation of the network topology over time. This allows us to distinguish a commonality in trends when considering other network filtering methods and the effects when using other financial instruments e.g. currencies and stocks.
Throughout the project, I was able to work with people from data science, economics and systems biology. Although we were based in different time zones, we were able to effectively coordinate with each other and produce some interesting results. Right now, we are continuing this work beyond the workshop towards a publication.
This experience improved my skills as a researcher and in engaging with a new online format. Although working online has brought new challenges, I believe this gave me the opportunity to explore a new area of mathematics and collaborate with others. I think that the economic impacts of COVID-19 will be thoroughly discussed in the coming years and I hope this work contributes to that discussion.
For further interest, you can watch a small talk given by myself and my collaborators during a workshop, which is titled “A minimum spanning tree approach to bond yields in COVID-19” under the section Parallel 6.
For details about myself please visit my academic webpage: http://personal.lse.ac.uk/PANGR/
References
Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical Society, 48-50.
Mantegna, R. N. (1999). Hierarchical structure in financial markets. The European Physical Journal B-Condensed Matter and Complex Systems, 193-197.
You can also read the most recent work of Raymond Pang (et al) on ‘An analysis of network filtering methods to sovereign bond yields during COVID-19′. It is available with free access until Friday 4 June 2021.