An interview with Paul Dütting on the Federal Communications Commission Incentive Auctions, Paul was an LSE Fellow in the Department of Mathematics in the academic year 2014-2015. He is now a Senior Researcher at ETH Zürich. Visit Paul’s homepage to learn more about his research on Algorithmic Game Theory, or to download his article on spectrum auctions and the SET for BRITAIN poster.
An interview with Paul Dütting on the Federal Communications Commission Incentive Auctions, Paul was an LSE Fellow in the Department of Mathematics in the academic year 2014-2015. He is now a Senior Researcher at ETH Zürich. Visit Paul’s homepage to learn more about his research on Algorithmic Game Theory, or to download his article on spectrum auctions and the SET for BRITAIN poster.
What is a spectrum auction? Why do we need to re-allocate rights, isn’t this question already settled?
Over the past decade many countries, including the UK, have run auctions to sell rights (licences) to transmit signals over specific bands of the electromagnetic spectrum. Now most of the spectrum is sold, but the demand for mobile internet is growing rapidly.
This has prompted the US government—and it is likely that other countries such as the UK will follow—to commission its spectrum agency (the Federal Communications Commission (FCC) in this case) to organise a double auction. In this auction the FCC will first buy back licences from TV broadcasters so that the remaining licences can be repacked into a smaller band; it will then sell the freed spectrum to mobile internet providers. The US Congressional Budget Office expects to spend about $15bn in the first phase, and it is hoping to collect up to $40bn in the second phase.
It has also already been decided how these auctions will proceed. Both phases will be iterative clock auctions, with a descending clock in the first phase and an ascending clock in the second phase [Milgrom and Segal 2014].
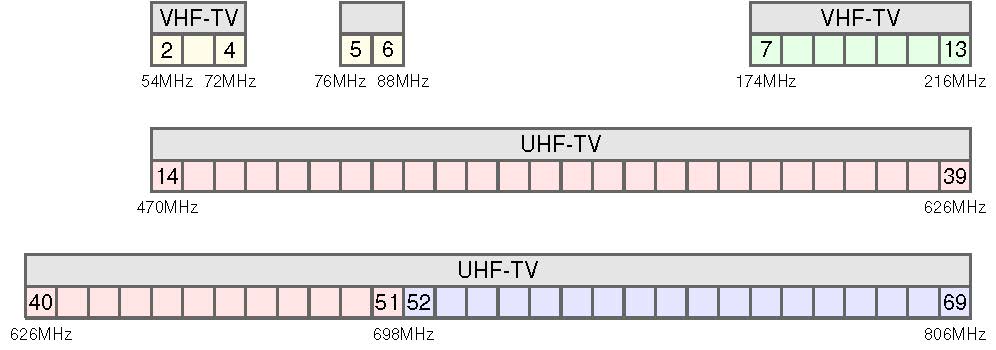
Currently, analog and digital TV stations are allocated to Channels 2–69. After the transition, digital TV stations will be assigned to Channels 2–51. Channels 52–69 will be reclaimed for advanced wireless uses.
So how do these clock auctions work, say the descending clock auction for the buy-back phase?
The FCC will have a target, that is, how much of the spectrum it would like to reclaim. It will then approach all license holders with an initial price for their license that is chosen at a high enough value that they will find it acceptable. These initial prices need not be the same for all license holders. Then, over a sequence of rounds, the FCC will decrease these prices. In each round the bidders are asked whether they want to stay in the auction or whether they want to drop out. This process is continued as long as it is possible to free the desired amount of spectrum by buying the licences of the bidders still in the auction. When deciding whether enough spectrum has been freed, it is possible to “compress” the stations that want to keep their existing licenses into fewer channels by re-assigning them to different channels.
Whilst, in principle, the question “Can we repack stations?” is one of the notoriously hard problems in Computer Science (known as Graph Coloring), state-of-the-art algorithms for solving this problem have proven proficient in answering this question reasonably quickly in practice [Leyton-Brown et al. 2016].
We have 8 stations (A–H) assigned to three channels (Red, Blue, and Yellow). We would like to repack these stations into two channels so that no two stations from the same channel overlap. It turns out that this is impossible without taking a station off air. However, after taking station H off air off air we can reassign A, C, F to Blue and B, D, E, G to Red.

Ok, that’s good news. Another important question is how should we decrease the prices in the buy-back phase?
Interestingly, Milgrom and Segal [2014] showed that this question boils down to a purely algorithmic one: for an allocation rule to be implementable as an iterative clock auction it is necessary and sufficient to use a reverse greedy algorithm. For the second phase, where the FCC seeks to sell licences, reverse greedy algorithms proceed as follows: initially, all bidders are “active” which means that they are tentatively accepted. Accepting all bidders, however, will typically not correspond to a feasible allocation because it will generally be impossible to assign all of them to the freed spectrum. The algorithm therefore proceeds by iteratively rejecting “active” bidders. A rejected bidder becomes “inactive”. Which bidder is rejected next is decided by scoring functions that assign each “active” bidder a score, and the lowest scoring bidder is the one that is rejected next. This rejection process is repeated until it becomes feasible to accept all remaining “active” bidders to the spectrum that has been freed in the first phase.
The tricky part is that only certain scoring functions are viable. Each bidder can have a different scoring function and the scoring functions can change from round to round. In any given round a bidder’s score should only depend on his/her own bid and the bids of other “inactive” bidders, but it is not allowed to depend on the bids of other “active” bidders. Another requirement is that the scoring function of a bidder is increasing in his/her bid.
In other words, if we want to understand how good the proposed auction format is, then we need to understand how good these reverse greedy algorithms are.
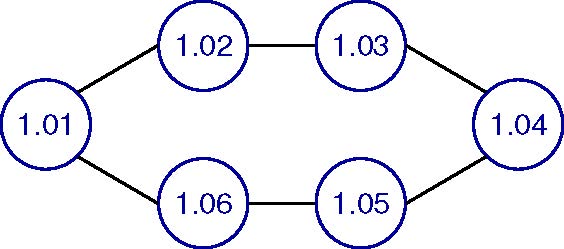
Here is an example. Let’s, for simplicity, assume that in the first phase we have freed a single channel. Now there are six wireless internet providers that seek to buy a license. In the graph below we represent each bidder by a node. The numbers correspond to the bidders’ valuations for being accepted. Our goal is to choose a subset of the bidders of maximum value. An edge between two bidders means they cannot be assigned to the same channel. So we have to choose a subset of bidders with no edges between them. In the example we can either accept one, two, or three bidders. Solutions with three bidders have higher value than solutions with fewer bidders. Out of the two possible solutions with three bidders the one with bidders 1.06, 1.04, and 1.02 has higher value. So this is the optimal solution, and its value is 1.06 + 1.04 + 1.02 = 3.12. Now consider the simple reverse greedy algorithm that uses the bidder’s value as their score. This algorithm would first reject bidder 1.01, then bidder 1.02, and so on until only the bidder with value 1.06 is left. The total value achieved by this reverse greedy algorithm is 1.06, which is considerably worse than the optimal solution.
As a trained Computer Scientist you’re in a good position to answer this question. Is the proposed format a good idea?
It certainly depends on whether well-designed reverse greedy algorithms are used. In recent work with Vasilis Gkatzelis (UC Berkeley) and Tim Roughgarden (Stanford University), for example, we showed that simply taking a succesful forward greedy algorithm and reversing the order in which it proceeds typically fails badly. In fact, we showed that many natural heuristics do not work.
We also showed that for so-called Knapsack auctions, in which m identical items are for sale and each bidder has a value of vi if he/she receives at least si items, no reverse greedy algorithm can achieve an approximation ratio better than O(log(m)). This is considerably worse than the approximation guarantee offered by the best forward greedy algorithm, let alone the approximation guarantee of the best possible polynomial-time algorithm.
On the other hand, we were able show that for the canonical single-minded combinatorial auction problem, in which m non-identical items are for sale and each bidder has a value vi if he/she receives a (super)set of a specific bundle of items Si, carefully designed reverse greedy algorithms not only match the approximation guarantees offered by the best known forward greedy algorithms [Lehmann et al. 2002], but they also provide the best possible approximation guarantee among all polynomial-time algorithms.
This is the result that you presented at SET for BRITAIN?
Yes, this is the result that I presented. It was great to see that politics and policy makers seek the exchange with research, and it seemed as if this work was particularly suited for such an event. In the end, it is Government policy makers who will decide on whether to run such an auction or not and if they do which format they want to use. However, as scientists we can do our part by informing this decision process.
Of course, there is nothing specific about spectrum auctions. There are, indeed, many problems in which both strategic thinking and algorithmic reasoning are required. Just consider Google’s success with Sponsored Search Auctions or up-and-coming platforms such as Uber. Both services would not be thinkable if it wasn’t for algorithms that would decide which ad to show at which price or what you have to pay for a cab ride.
It is this general field—called Algorithmic Game Theory—that fascinates me and that I explore in my research.