Peter Allen, Julia Böttcher and Jozef Skokan are in the discrete mathematics group of the Department of Mathematics at the London School of Economics and Political Science. They organised a workshop on “Large-scale structures in random graphs” in December 2016 which was hosted at Alan Turing Institute and generously jointly funded by the Heilbronn Institute and the Alan Turing Institute. Their write up of the event is produced below.
While much of the rest of London was busy Christmas shopping, around 25 mathematicians (some from as far away as Brazil, the US and Israel) spent the week of 12-19 December 2016 on what mathematicians are accustomed to do: thinking – or rather thinking and discussing. Only this time the locus of this thinking was the side-wing of the British Library that is the new and shiny Alan Turing Institute. And the mathematicians met for a workshop on “Large-scale structures in random graphs”, organised by three LSE academics (Peter Allen, Julia Böttcher and Jozef Skokan), and funded jointly by the Heilbronn Institute and the Alan Turing Institute.
What does this look like?
Well, in the mornings there were lectures; and there was coffee, of course (the great Hungarian mathematician Paul Erdős famously said that “Mathematicians are machines for turning coffee into theorems”). The afternoons were spent discussing in small groups, scribbling formulas and sketching pictures on boards, walls, and meeting room glass panes. (Yes, the Alan Turing Institute has white-board walls and special markers for writing on glass. Coffee, by the way, comes out of what looks like an ordinary tap, operated via a tablet.)
It was an intense and highly successful workshop, pushing further the boundaries of what we currently know in the area. And it concerned an important topic: the study of how certain types of large networks form and what we can mathematically say about their global structure, albeit having only very limited local information. In the current age, where a vast amount of data is shared on large networks (such as the internet or Facebook), it is vital to acknowledge that, unsatisfactorily, there are still many features of even simplified mathematical models underlying such networks that we do not adequately understand.
But what was the workshop really about?
We will now try to give you some insight into this. We should start by explaining some of the words appearing in the title of the workshop.
What is a graph?
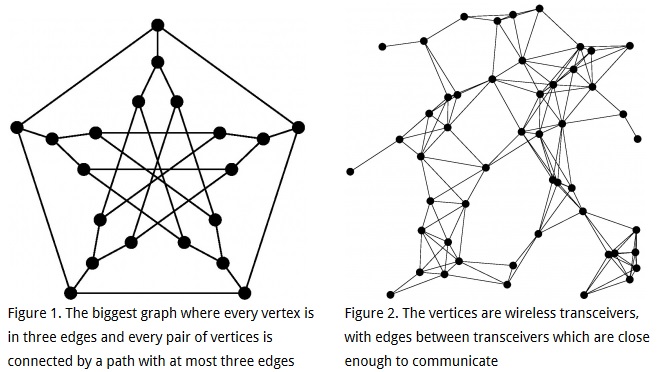
The word ‘graph’ means two things in mathematics. One is the familiar x-y plot which shows us, for example, how much more expensive Euros have become since Brexit. The other, which is an abstract representation of two-body interactions, is what this workshop is about (see Figure 1). A graph has vertices (representing the interacting bodies), some pairs joined by edges (representing an interaction) and others not. Think of a social network in which people (vertices) may be friends (an edge is present) or not; or a road network where places are connected by roads (and in this example some edges, the one-way streets, come with a direction (see Figure 2)). We usually think of graphs visually, drawing points for the vertices and lines between two points for the edges.
What is a random graph?
A misnomer, really: it’s not ‘a graph’. What we mean is a way of generating graphs which uses some randomness. Most simply, we decide on the number n of vertices we will have, and then for each pair of vertices we flip a coin to decide whether to put an edge in or not (so we will do a lot of flipping coins). In this case, each pair of vertices will turn out to be an edge with probability ½, independently. There are (many) other options. We could use a biased coin, which gives us an edge with some fixed probability p not necessarily equal to ½. This method of generating random graphs is called G(n,p), and it is the method most time was spent on, both in mathematics in general and at the workshop. There are many other methods one could choose, either because they are supposed to model some real-world phenomenon or because they are mathematically interesting, but even after 60 years of research there are still many things about the simple G(n,p) model that we do not understand.
What can you say about random graphs?
The kind of thing we end up writing formally are sentences like ‘With high probability a random graph generated according to G(n,p) is connected’. The word ‘connected’ means what it sounds like: you can get from any one vertex to any other by following edges. And ‘with high probability’ means that, as the number n of vertices gets large, the probability gets closer and closer to one. Informally, we would say ‘A typical random graph G(n,p) is connected’; if you actually follow the random method G(n,p) of generating a graph, the graph you end up with is very likely to be connected.
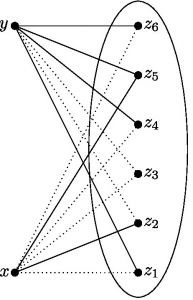
To get a feel for how things work in this area, let’s try to explain why this statement is true, for a fair coin (p=1/2). We’ll try to argue that not only is there a way to get from any x to any other y, actually we can even always do it using exactly two edges. We start off with our n vertices. Let’s call two of them x and y. We want to know, to start with, how likely it is that x and y are connected using exactly two edges when we generate G(n,p). In other words, we want to know how likely it is that there is some z such that xz and zy are both edges (see Figure 3). Apart from x and y, there are n-2 other vertices, so there are n-2 choices for z.
If we fix any given one of these, the chance that xz and yz both appear in G(n,1/2) is 1/4 – the chance of getting heads twice when we flip two coins, because that’s exactly what we do to decide whether these two pairs are edges. But if we look at all of the n-2 choices of z, there is that 1/4 chance each time; and the pair x,y only needs to get lucky once. The probability they don’t get lucky is (3/4)^(n-2). To fix an example, if n is 8,000, that is even more unlikely than winning the Lottery a hundred and fifty times in succession – we should be pretty confident that x and y turn out to be connected.
We want to know the whole graph is connected – ideally, we hope that every pair of vertices wins this little game (and let’s forget about all the other ways they might get connected; taking them into account can only help us find connections). There are lots of pairs of vertices – roughly n^2/2. It’s easy to check that n^2/2 grows much more slowly than (3/4)^(n-2) shrinks, so on balance, you should be amazed if even one single pair of vertices loses its little game when n is large. Returning to the n=8,000 example, in this case n^2/2 is about 32 million; about as many people as play the Lottery each time. No-one has ever even won the Lottery twice on consecutive draws, let alone a hundred and fifty times – so you should believe, at least for n=8,000, that it’s clear G(n,1/2) is very likely to be connected.
There is a subtlety here: these little games are not independent; every pair x,y is playing as part of the one big game of constructing G(n,p), just as when many people play the Lottery, they all get results based on one set of balls drawn. When people play the Lottery, they could all choose the same numbers – then there would be a very low chance of anyone winning. Or they could all choose different numbers – this makes it as likely as possible that someone will win. With 32 million people, they can actually choose all the possibilities and be sure of someone winning. If we knew how all the players in the Lottery chose numbers, we could calculate the chance that there will be a winner – the answer is somewhere between 1 in about 14 million (if everyone picked the same numbers) and certain (if all the players conspired to all choose different numbers). Similarly, it’s easy to find out how likely it is that a given pair x,y loses the little game and turns out not to be connected by a two-edge path (not very!) but what we want to know is the chance that any one of all the about n^2/2 pairs loses. Just like with the Lottery, that could be anywhere from (3/4)^(n-2) up to (3/4)^(n-2).n^2/2, depending on how the little games overlap. The right answer is somewhere between these extremes, but it gets hard to calculate. If I tell you that there is a connection from x to y, you should be more confident there is one from x to some other vertex w as well, for example. But in this example, it’s enough to know that the probability of losing in some little game can’t be bigger than (3/4)^(n-2).n^2/2 .
That doesn’t seem so hard..?
This example isn’t hard, but the reason is that we could get away with being lazy doing calculations. We wanted to show that typically G(n,p) is connected; we can get from any one vertex to any other. It turned out to be enough to look only at connections using exactly two edges (not one, not three, not more) to convince ourselves that this is likely, which made our lives easier. And it turned out to be enough to pretend the little games of connecting each pair x,y were conspiring to make our lives hard – a bit like the players of the Lottery conspiring to all choose different numbers so that there is a winner for certain – even though we know that’s not really the case. We were playing a game with the odds stacked heavily in our favour. So let’s make it harder, and consider G(n,p) with some p much less than 1/2. Now we flip a biased coin to see whether each edge appears; we expect to get far fewer edges, and of course if we have less edges then (intuitively) it should be less likely we will get a connected graph. What we would really like to know is the ‘threshold’: how small can we make p be and still be fairly confident of getting a connected graph (with say probability 99%)?

This is too hard to answer properly in a blog post. In fact, it’s getting closer to some open problems in the area – one of our speakers, Asaf Ferber, talked about some exciting new progress.
You could now skip to the next section – but if you want a vague idea of what the answer to this ‘threshold’ problem is, here is a vague explanation. One thing we can say is, if we want to be confident that G(n,p) is connected, we should certainly be confident that every vertex is in at least one edge: if a vertex isn’t in any edges, we can’t go anywhere from it and we certainly do not have a connected graph. It turns out this gives the answer: if p is large enough that with 99.5% probability every vertex is in at least one edge, then also with 99% probability the whole graph G(n,p) will be connected (when n is large, anyway). To see why this is true, you could try to re-do the explanation above, but consider connecting paths of all lengths (not just length two) between each x and y. Working out how likely it is that even one pair x,y wins its little game gets hard – but if you make life easier by throwing away possibilities as we did above, then what happens is that you probably threw away all the paths connecting x and y, so you don’t see that you won (like turning off the television half-way through the Lottery draw). Then you would have to put all these little games together, and this time you would have to work out how much they overlap – the worst case we used above, pretending that they were conspiring against us, won’t work this time; you would end up thinking you are very unlikely to get a connected graph, even though that’s not the case. It turns out these little games do conspire a bit, but not much. Actually, trying to do this whole calculation gets too complicated for anyone to solve. We do know the answer, but we use a different route to get to it – roughly, rather than trying to find paths connecting each pair of vertices, we start by arguing that if the graph is not connected, then that means it splits into two parts with no roads between – like the Irish Sea between the street-maps of Britain and Ireland – and show that oceans don’t tend to show up in random graphs.
More or less, this is where all the difficulty is in studying random graphs. Even though the edges are independent – whether one pair turns out to be an edge doesn’t affect another, because one coin toss doesn’t affect another – the properties we want to know about tend to involve playing a lot of little games, each one of which we will easily win but which do depend on each other in some complicated way. It’s hard to figure out if we’re likely to win the big game by winning all the little ones.
What is this large-scale business?
We want to know about properties for which you have to look at the whole random graph (or at least most of it), like ‘being connected’. If you only look at part of the random graph, you don’t know whether it’s connected. The other extreme is asking a question like ‘Are there four vertices with all six possible edges present?’ – if the answer is yes, I can convince you just by showing you the right four vertices. Usually we can answer questions of this type quite well.
Another example is that we might want to know whether a travelling salesman can go round all the vertices of the graph, following edges, until they return to their start without ever having to revisit vertices on their way – this is called a Hamilton cycle.
Again, it’s not too hard to show that in G(n,1/2) the answer is yes; again, if we have less edges – if we look at G(n,p) for some small p – it obviously gets less likely. As with connectivity, obviously we need every vertex to be in at least two edges for this (otherwise the salesman goes in to a vertex that’s in only one edge and can’t go out again), and it turns out that if p is large enough that with probability 99.5% every vertex is in at least two edges, then with probability at least 99% we will have the Hamilton cycle.
What sort of things did we actually do in the workshop?
From the examples above, it sounds like we know a lot about how big p should be in order that we are confident that a specific structure shows up in G(n,p), like a Hamilton cycle. Actually, that’s not the case; for a lot of structures, not much more complicated than a Hamilton cycle, we don’t really know. We spent quite a bit of time working on a particular class of structures, ‘bounded degree graphs’, where we think we know what the answer could be. Some of the participants brought partial answers to the workshop, and putting them together it looks possible that a solution will come out.
What if the Highways Agency try to obstruct the travelling salesman by doing roadworks to cut him off? If they dig up too many roads leaving one town, the residents will complain to their MP – so the agency won’t do this. Can they still block the salesman? This sort of question is called a resilience problem. We know only a couple of techniques to work on this kind of problem, and a lot of the time they don’t work. We tried one of the simplest problems where the known techniques don’t seem to work, ‘tight Hamilton cycles in hypergraphs’. Some progress was made, but we did not yet get to a solution.

What about atypical random graphs? We expect about n^2/4 edges to show up in G(n,1/2); if there are many less, or many more, than that, then something weird happened. What does the result look like, and how likely is the weird event? In this case, the result looks like you accidentally used a biased coin: it looks like G(n,p) for some p not equal to 1/2, and we can calculate the chance of that happening easily. What about if we counted triangles instead? In this case, if there are too few triangles again G(n,1/2) probably looks like a typical G(n,p) for some p<1/2. If there are too many triangles, though, something else can happen: probably there are too many triangles because a little set of vertices gets far more edges than we expect, while the rest of G(n,1/2) still looks like a typical G(n,1/2). We don’t understand this sort of problem very well in general. Simon Griffiths and Yufei Zhao both talked about these problems, and two groups worked on different aspects. One group got results on their problem, the other made progress but still pieces are missing.


In another direction, Ramsey’s theorem says: for any graph H, there is a graph G such that however you colour the edges of G with red and blue, you will find a copy of H (plus maybe some extra edges) with either all edges red or all edges blue. Think for example of a path with n edges; there is a graph G which, however you colour the edges, will contain either a red or a blue path with n edges. How many edges does G need to have? It’s obvious that to get an n-edge path you need at least n edges in G; what number is enough? It turns out 100n will do. This problem is the size Ramsey problem; it doesn’t obviously have anything to do with random graphs. But there is a surprising connection: for many graphs (such as the n-edge path), the best graph G we know works is a typical random graph. But again we usually don’t know any very good answer; the path is one of the few graphs where we ‘only’ have a constant-factor gap between the lower and upper bounds. David Conlon‘s talk was about how to do better with proving that a random graph with few edges works in general, and the speaker set as a problem to show that path-like graphs – distance powers of paths – also have size Ramsey number growing linearly in n. Here it’s clear that a random graph on its own does not work: but the group working on this problem came up with a nice construction that modifies a random graph which they could show works, solving the problem.
We had several more talks and groups, which made good progress on more problems in this sort of spirit. But this piece is long and technical enough by now – to wrap up, we had a good week with excellent talks and productive sessions of group work; some of the results will be written up directly, while other groups will continue collaboration over the next months and years.