
Why do asset price bubbles in real markets happen? Experimental asset markets have pursued the reasons for a long time. Our research clarifies them by distinguishing between two effects, confusion and strategic uncertainty.
The asset price bubbles observed in real markets are often regarded as irrational exuberance, as pointed by Professor Robert Shiller (Nobel laureate in 2013). However, we succeed in identifying another mechanism at work from asset price bubbles observed in experimental markets. Based on our experimental finding, we conclude that asset price bubbles consist of both rational and irrational exuberance, and these two exuberances are equally important.
Experiments in economics and finance are a new innovative methodology. This methodology allows researchers to create various economic environments while opening up or shutting down the channels through which the effects under investigation operate. Furthermore, the participants in economic experiments make decisions that have real monetary consequences. At the end of the experiment, they would receive cash prizes according to their performances measured based on the pre-specified rules of the experiment!
In our experiments, we consider hypothetical asset markets where standard economic theory predicts that bubbles cannot happen. In our experiments, participants know all the relevant aspects of the market, such as how many other participants there are, how many assets are to be traded, and how much money they initially hold. In addition, they also know how many periods they trade in the markets, and have enough information to compute how much the fundamental value (FV) of an asset is in each period.
However, the pioneering work by Professor Vernon Smith (Nobel laureate in 2002) and his colleagues, and many other studies that followed, have demonstrated that bubbles do happen even in such organised experimental markets where subjects can identify the fundamental value of an asset. Puzzled by this, recent studies have tried to understand the cause of bubbles by positing the ‘irrational exuberance’ or ‘confusion’ of non-rational participants such as participation motivations, and insufficient understanding of experiment instructions, as the main driving force. On the other hand, we shed light on a different aspect, strategic uncertainty which is the difficulty of predicting others’ behaviour.
Our hypothesis conjectures that rational participants may behave as if they are confused because they doubt the rationality of other participants. If rational participants consider others’ behaviour irrational, they try to take an appropriate action taking such irrational behaviour into account. In that sense, the researchers may take rational exuberance for irrational.
Our experiment distinguishes between confusion and strategic uncertainty as follows: We created two different experimental asset markets: One consists of six human traders (6H treatment), and the other consists of one human and five computer traders (1H5C treatment) as shown in Figure 1.
Figure 1. Two treatments
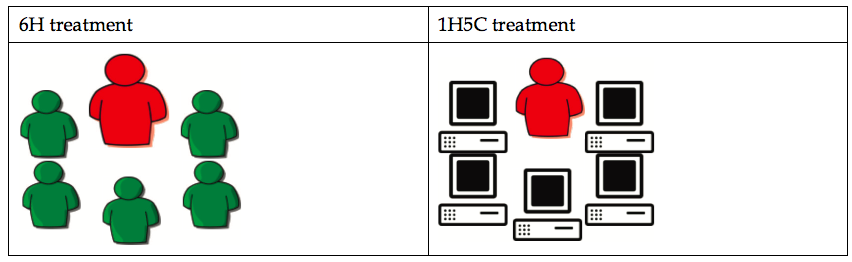
The participants in the experiments were informed about the nature of the other traders in the market in which they were participating. While those in the 6H market knew that there were five other human participants in their market, those in the 1H5C market knew that there were no other human participants but only five computer traders were present in their market.
Furthermore, these participants in the 1H5C market were informed that all the five computer traders submitted the buy/sell orders at the fundamental value of the asset in each period. Note that in 1H5C treatment, prices will follow the FV of the asset in each period due to the behaviour of the computer traders, while prices in 6H treatments may not. Therefore, comparing the realised prices between 6H and 1H5C treatments will not allow us to distinguish between the effects of irrational and rational exuberance.
The key to successful distinctions is to give the subjects monetary incentive to accurately predict future prices, and to compare their forecasts between the two treatments. In both treatments, at the beginning of each period we asked participants to forecast the future prices of all the remaining periods. If some of their forecasts of future prices were accurate, the participants were given bonus payments according to the numbers of correct predictions of the future prices; i.e., the predictions that were within 10 per cent of realised prices.
The participants in 1H5C knew that other traders in their market (i.e., computer traders) submit orders at fundamental value in each period. Thus, if they were rational and not confused, they should forecast the prices to follow the asset’s FV in each period. If there were any deviations of their price forecasts from the FVs, however, this is a result of the participants’ confusion.
In 6H, in contrast, rational and non-confused participants may forecast prices that deviate from the FVs because of the strategic uncertainty they face. Of course, it is also possible that participants’ forecasts deviate from the FVs due to their own confusion just as in 1H5C treatment. Therefore, by comparing the deviation of price forecasts from FVs in these two treatments, we can distinguish the effect of subjects’ confusion and strategic uncertainty
We have constructed a measure of the absolute deviation of price forecasts from FVs that we call RAFD, and compared the RAFD of the first set of price forecasts submitted by participants in two treatments. Figure 2 shows the empirical cumulative distributions of RAFD. The larger RAFD indicates the larger difference between forecasts and FVs, and no difference when it is zero. The outcomes from 1H5C are shown in blue and those from 6H are shown in red. As one can see, the latter lies on the right of the former, demonstrating that indeed the initial set of price forecasts deviated more from the FVs in 6H treatments than in 1H5C treatment.
Figure 2. Empirical cumulative distribution of RAFD
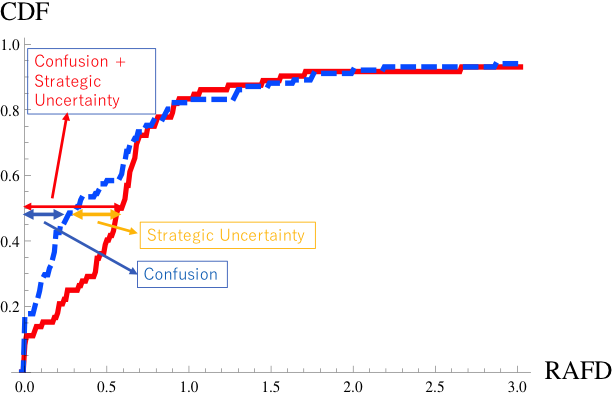
Created based on Akiyama et al (2017, Fig. 1)
Recall that, as we note in Figure 1, RAFDs in the 1H5C treatment represent the effect of confusion, while RAFDs in the 6H treatment represent the combined effect of confusion and strategic uncertainty. The gap between the two is, therefore, the effect of strategic uncertainty.
We find that both confusion and strategic uncertainty are equally important in the experiments. Thus, it is not just confusion, which has been the focus of existing studies, that causes bubbles in an experimental asset market. Strategic uncertainty also does as well.
Furthermore, we have administered a Cognitive Reflection Test (CRT) at the end of our experiment. CRT consists of a few questions such as “A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?” The score of this test measures participants’ tendency to override impulsive and non-reflected responses. We found that while the participants’ scores on the CRT were negatively correlated with the measured effects of confusion (compare the difference in the blue lines between the two panels in Figure 3), there was no such correlation between the CRT scores and the total effect of confusion and strategic uncertainty (compare the red lines in the two panels in Figure 3). This means that those who are less confused are more sensitive to the presence of the strategic uncertainty that is present in the market, demonstrating an interesting interaction between rational and irrational exuberance.
Figure 3. Empirical cumulative distribution of RAFD in 6H and 1H5C treatment, depending on the CRT Score
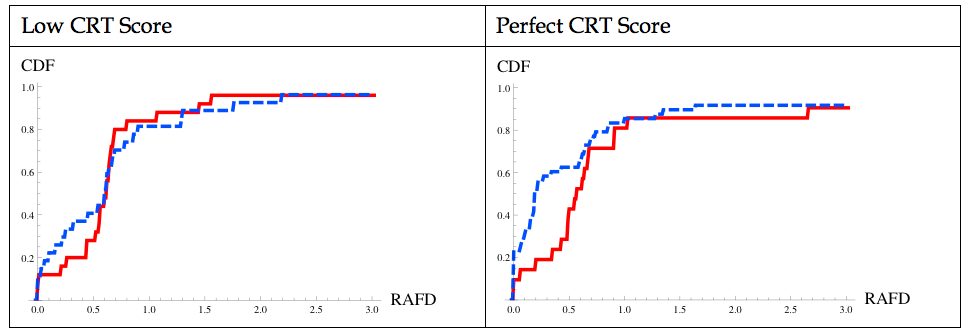 Source on Akiyama et al (2017, Fig. 2, panel (a) and (c))
Source on Akiyama et al (2017, Fig. 2, panel (a) and (c))
♣♣♣
Notes:
- This blog post is based on the author’s paper It is Not Just Confusion! Strategic Uncertainty in An Experimental Asset Market, co-authored with Eizo Akiyama and Ryuichiro Ishikawa, The Economic Journal, October 2017.
- The post gives the views of its author, not the position of LSE Business Review or the London School of Economics.
- Featured image credit: Bubble bursting, by Duncan Rawlinson – Duncan.co – @thelastminute, under a CC-BY-NC-2.0 licence
- When you leave a comment, you’re agreeing to our Comment Policy.
 Nobuyuki Hanaki is a professor of economics at Université Côte d’Azur, France. He is a member of GREDEG, a research group jointly funded by Université Côte d’Azur and CNRS. After receiving Ph.D. in economics from Columbia University, he taught at the University of Tsukuba, Japan, and Aix-Marseille University, France, before joining Université Côte d’Azur. He was a junior member of L’Institute Universitaire de France between 2011 and 2016. His research focuses on understanding the consequences of interactions among heterogeneous agents, with such methodologies as experiments, mathematical and computational modelling. He is the principal investigator of a research project called “Behavioral and Experimental Analyses in Macro-Finance” (BEAM) jointly funded by French, German, Dutch, and Japanese science foundations.
Nobuyuki Hanaki is a professor of economics at Université Côte d’Azur, France. He is a member of GREDEG, a research group jointly funded by Université Côte d’Azur and CNRS. After receiving Ph.D. in economics from Columbia University, he taught at the University of Tsukuba, Japan, and Aix-Marseille University, France, before joining Université Côte d’Azur. He was a junior member of L’Institute Universitaire de France between 2011 and 2016. His research focuses on understanding the consequences of interactions among heterogeneous agents, with such methodologies as experiments, mathematical and computational modelling. He is the principal investigator of a research project called “Behavioral and Experimental Analyses in Macro-Finance” (BEAM) jointly funded by French, German, Dutch, and Japanese science foundations.

