Donald Trump’s 2016 election victory took many by surprise – most of the polling had suggested a victory for Hillary Clinton. But were the polls wrong? In new research Manfred te Grotenhuis, Subu Subramanian, Rense Nieuwenhuis, Ben Pelzer and Rob Eisinga examine the election polls’ accuracy by randomly sampling from each state’s observed voters for Clinton or Trump. They find that a relatively small polling bias which saw Republicans underrepresented in a number of key states tipped the polling – and therefore the predicted probability that she would win – in favor of Hillary Clinton.
Ahead of Election Day in 2016, the statistics and polling analysis site FiveThirtyEight gave former Secretary of State Hillary Clinton a 70 percent probability to win the presidential election. This prediction was based on an average of many US polls. According to the American Association for Public Opinion Research (AAPOR) this prediction turned out to be incorrect because of a) a real change in voters’ preferences just before the election, b) an overrepresentation of college graduates in some poll samples and c) late-revealing Trump voters.
What has been generally overlooked is that the polls leading up to the election actually did not perform so badly at all. For instance, the state-level predictions of FiveThirtyEight were in agreement with the actual electoral outcomes for no less than 45 US states plus the District of Columbia. If we sum all electoral votes in these states we get a virtually neck and neck result of 231 votes for Trump and 232 for Clinton. In Florida, Michigan, Pennsylvania, Wisconsin, and North Carolina FiveThirtyEight had predicted wrongly. Apart from North Carolina, in these states the electoral margins were extremely narrow. For instance in Michigan 47.5 percent of all votes went to Trump and 47.3 percent to Clinton! Those narrow electoral margins probably made it hard to predict the outcome in a reliable way given the sample sizes polls used. This is important to note because the 2016 US presidential election was won in Florida, Michigan, Pennsylvania, and Wisconsin with their decisive total of 75 electoral votes.
In a perfect world, polls sample from the population of voters, who would state their political preference perfectly clearly and then vote accordingly. However, results from small random samples can be quite unreliable due to extremely narrow electoral margins. To calculate the probability of winning the 2016 US presidential election in that perfect world, we drew 1 million random samples (with a reasonable sample size of 1,500) from each of the four key state’s observed votes for Clinton, Trump, and other candidates. Next, we counted the number of random samples with the most votes for Trump and the number of samples with Clinton as the winner.
In Florida, about 677 out of every 1,000 random samples had Trump as a winner, 314 samples favorited Clinton, and 9 samples turned out to be inconclusive. Next to Florida, we calculated the probability of a Clinton victory in Michigan at 46 percent, and both Pennsylvania and Wisconsin at 39 percent, again after drawing a million random samples per state from the known population of voters. Recall that Clinton already had 232 votes from the other states + DC, and thus needed another 38 electoral votes to become the first female US president. This implies she had to win Florida plus at least one of the other three battleground states or win in Michigan, Pennsylvania, and Wisconsin. To illustrate: Hillary Clinton had a 2 percent (.314 x .463 x .387 x .385) predicted probability of winning all four states. The probability, then, of winning the 2016 presidential election is the sum of all eight winning combinations and amounted to 29 percent. For Donald Trump, the eight paths to victory added up to 67 percent. To get a notion of how heavily the predicted probabilities depend upon sample size, we calculated the probabilities for Clinton to win for sample sizes between 100 and 5,000 (see Figure 1).
Figure 1 – The estimated probability of a Clinton victory using random samples from the actual 2016 US presidential election results
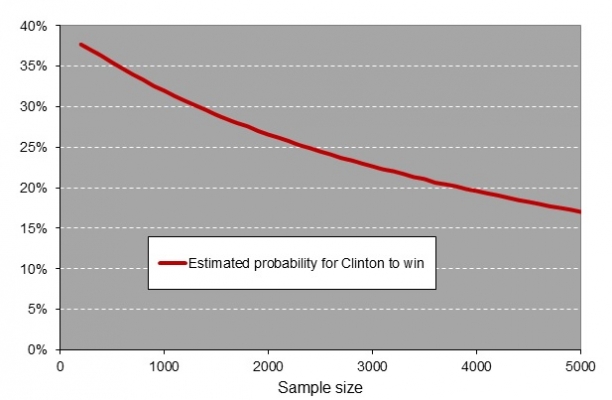
The estimated probability for Clinton to win is not much higher than 35 percent in the graph above. With random samples of 1,500 voters per state it is around 30 percent. This number indicates that on average we will incorrectly predict Clinton as the winner of the 2016 US election 3 out of 10 times when random samples of 1,500 are used. On the basis of these calculations, the narrow 2016 electoral margins in the four battleground states are not a large threat to the validity of the polls’ predictions.

“#clinton as #trump” by Oli Goldsmith is licensed under CC BY SA 2.0
Next we investigate the effect of small sampling bias on the polling results in the four crucial battleground states. Clinton was predicted to win the popular vote (i.e. the total number of votes) with a difference of about 3 percent while in reality this was close to 2 percent. Under the assumption that this 1 percent bias is state-independent, we added this number to the actual electoral outcomes. To illustrate: in Pennsylvania Clinton received 47.9 percent of the votes and Trump 48.6 percent. So we increased the population of Democrat voters to 47.9 + 1 = 48.9 percent. Consequently the population of Republication voters was decreased to 48.6 – 1 = 47.6 percent. Next, we randomly drew 1 million random samples per state from these 1 percent biased populations and recalculated the overall probability to win the elections. This rather small sampling bias made the predicted probability of 70 percent for Trump to win change into a 30 percent win, a prediction more or less in line with most polls’ predictions just before Election Day.
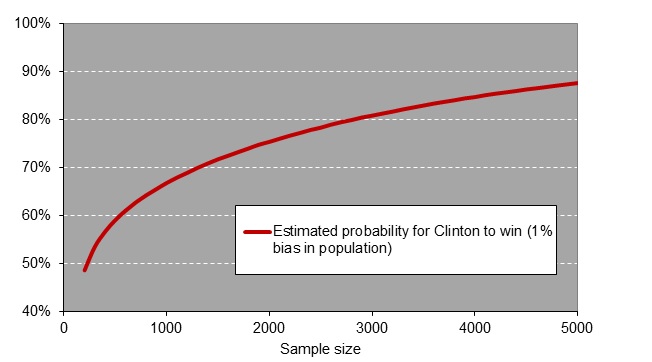
Next, we calculated the chances of a win for Clinton for all sample sizes between 100 and 5000, after taking into account a 1 percent bias. As can be seen in Figure 2, the wrong prediction rapidly increased as the sample size rose. So, with large samples almost in 9 out of 10 times Clinton is falsely predicted to be the winner of the elections. This makes perfect sense: the 1 percent bias in Democratic voters is detected well by these large samples, consequently Clinton received the false favorable odds of winning the elections.
Figure 2 – The estimated probability of a Clinton victory using random samples drawn from the 2016 US presidential election results + a 1 percent Democratic bias.
The importance of quality poll samples when margins are narrow
In the last US presidential election polls handed Clinton a fair chance to win the elections. The explanation for this mishap probably is not small sample sizes or too narrow electoral margins as such. The point is that the polls very likely sampled from a population that just was not sufficiently representing Republicans. In most states that small representation bias was of no importance as the electoral margins were wide enough. However, in four crucial battleground states with a large reservoir of electoral votes, margins were very narrow and enabled the small bias to dramatically tip the scale and made the polls predict the overall odds in favor of Clinton.
When things get this tight again, high quality samples are needed, which are far more representative of the US voters than the 2016 samples. However, even highly representative samples cannot repair the bias of late changes in political preferences and late-revealing. They will always be a snapshot of a population that for some part has not fully made its mind up yet. We have to realize that political polls at best are a fair prediction at some point in time and may constitute a wrong forecast of the actual election result, just because one candidate may have a larger share of late-revealers than the other. With this in mind both pollsters and the media may have been a little too self-assured when they presented the results of yet another US 2016 election poll.
- For further details see http://www.ru.nl/sociology/mt/sig/downloads.
Please read our comments policy before commenting.
Note: This article gives the views of the author, and not the position of USAPP – American Politics and Policy, nor the London School of Economics.
Shortened URL for this post: http://bit.ly/2nxIHbn
_________________________________
About the authors
 Manfred te Grotenhuis – Radboud University
Manfred te Grotenhuis – Radboud University
Manfred te Grotenhuis is an associate professor of quantitative data analysis at Radboud University and an affiliate of the Interuniversity Center for Social Science Theory and Methodology (ICS). He does research and teaching in inferential statistics, age-period-cohort models, multilevel modeling, event history analysis, and SPSS syntax.
 Subu Subramanian – Harvard University
Subu Subramanian – Harvard University
S V Subramanian (“Subu”) is a Professor of Population Health and Geography at Harvard University, and Director of a University-wide Initiative on Applied Quantitative Methods in Social Sciences. He was also the Founding Director of Graduate Studies for the interdisciplinary PhD program in Population Health Sciences.
 Rense Nieuwenhuis – Swedish Institute for Social Research
Rense Nieuwenhuis – Swedish Institute for Social Research
Rense Nieuwenhuis is a is an assistant professor at the Swedish Institute for Social Research (SOFI). He is a quantitative sociologist interested in how the interplay between social policies and demographic trends gives rise to economic inequalities.
 Ben Pelzer – Radboud University
Ben Pelzer – Radboud University
Ben Pelzer is an Assistant Professor of Quantitative Research Methods at the Department of Sociology / Social Science Research Methods of Radboud University.
 Rob Eisinga – Radboud University
Rob Eisinga – Radboud University
Rob Eisinga is a professor of quantitative research methods at Radboud University. His substantive interests concern the analysis of social and political change, including electoral and religious behavior, and the obesity epidemic. His current methodological interest is in the analysis of rank data and their null distribution in particular.




I fail to see how all the heavy number crunching described in this study provides any useful information about what happened with the 2016 polls.
You don’t need to know much math or statistics to understand that simulations using actual voting records as their input are going to “predict” how voters actually voted. That is of no use whatsoever in making predictions before the vote as to how voters will vote at some future time.
In their last paragraph, the authors fall back on the admission that it’s just hard to predict any close election from polls, but the point was made much more pointedly by the Mosteller committee 68 years ago:
“The pollsters overreached the capabilities of the public opinion poll as a predicting device in attempting to pick, without qualification, the winner of the 1948 presidential election. They had been led by false assumptions into believing their methods were much more accurate than in fact they are. The election was close. Dewey could have won by carrying Ohio, California and Illinois which he lost by less than 1 percent of the vote. In such a close election no polls, no advance information of any kind, could have predicted a Truman or Dewey victory with confidence.”
Dear Jan,
Thank you for your comment. I do not agree that taking samples from the actual population is not useful here. As you may note from the first figure, the odds are roughly 3 to 7 for Clinton to win in case samples of n=1,500 are being used. We now have a base line to make further comparisons to. The idea that narrow margins as such were the cause of predicting wrong is thereby NOT corroborated. After adding the small bias the odds turned into a 7 to 3 victory for Clinton, a finding in line with most predictions. The warning from 68 years ago relates to narrow margins as such if I‘m not mistaken. In the 2016 election it were not narrow margins as such that caused all the damage but non-representative samples which were harmful in case the margins were narrow. That is the take home message.
Best regards,
Manfred
Ya think????