Norman Biggs is Emeritus Professor of Mathematics at LSE. He is the author of 13 books and over 100 papers on Mathematics, and has also published in the fields of Numismatics and Metrology. His latest book, “Quite Right: The Story of Mathematics, Measurement, and Money” was released in February 2016.
Norman Biggs is Emeritus Professor of Mathematics at LSE. He is the author of 13 books and over 100 papers on Mathematics, and has also published in the fields of Numismatics and Metrology. His latest book, “Quite Right: The Story of Mathematics, Measurement, and Money” was released in February 2016.
I’m not an astronomer and I do not understand cuneiform script, so what follows must be read with that in mind. The subject of this blog is the recent discovery that a Babylonian clay tablet, dating from before the Christian era (between 350BC and 50BC), contains material that resembles ‘calculus’. The headline in the Independent (29 January 2016) was written to arouse interest: ‘Calculus Babylon! Ancient scholars used abstract geometry to track path of Jupiter’.

My suggestion is that the tablet is an example of a method that was often used in ancient times for a more down-to-earth purpose. The same method was also used in the early modern period, when the subject we know today as ‘calculus’ was being developed mathematically.
Suppose you were an ancient astronomer observing the movement of Jupiter daily for a number of consecutive days. You would choose some appropriate unit (probably an angular distance), and find that on the first day it moves 3 units, on the second day 2 units, and so on. For simplicity, suppose you give up after five days, having recorded the numbers 3, 2, 2, 1, 2 units. Then you would be able to work out that the total movement of Jupiter was 3+2+2+1+2 = 10 units.
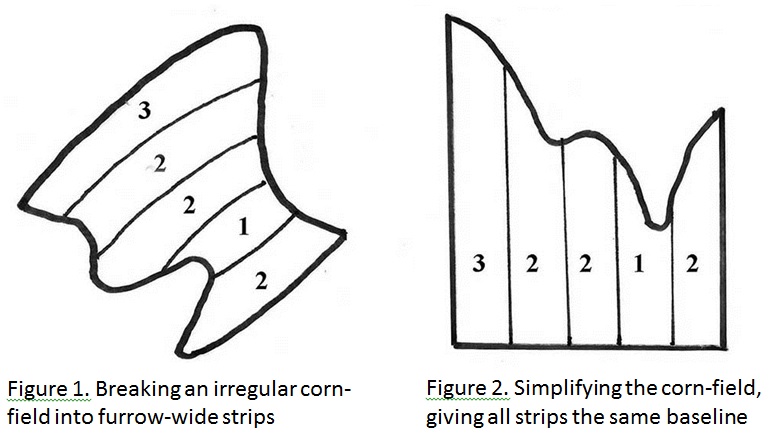
Now, you might recognise that this simple method of working out the total is also used in another, more routine, situation: measuring the size of your corn-field. Your ploughman (with his team of oxen) will plough the field by making strips, each of one furrow’s width. From ancient times this has been the basis of a rough method of assessing the size of the field, and has bequeathed to us words like furlong. Derived from the Old English furh (‘furrow’) + lang (‘long’), this word originally denoted the length of furrow that could be ploughed by a team of oxen without stopping (we won’t go into the possible inconsistencies of this measurement here). So the ploughman could note (using a tally-stick if necessary) that in ploughing the first strip, along one side of the field, the team had to stop three times, indicating that three furlongs had been covered. The next strip might be measured as two furlongs in the same way. If your field was typically irregular, as in Figure 1, being bounded by streams for example, the tally record might show that there were five strips of 3, 2, 2, 1, 2 furlongs. (Of course, the picture has been distorted for the sake of clarity: in reality a furrow is about 20 centimetres wide, and a furlong is about 200 metres long.)
Does this suggest to you a method of representing the movement of Jupiter by a picture that looks quite like your field? You could simplify the picture by lining up the strips so that they all stand on the same baseline, and their sides are straight. In that case the strips become ‘trapeziums’, and you have a picture like Figure 2.
In the seventeenth century mathematicians began to try to calculate the areas of irregular figures using symbolic algebra, a fairly new mode of working at that time. They used the old strip-method. For example, John Wallis used it to calculate the area of certain figures that are bounded by one curved line and three straight lines, like that in Figure 2. Not long afterwards, Isaac Newton made a remarkable observation. He noticed that, quite generally, areas could be found by a method based on regarding the curved boundary as representing the speed at which some quantity is changing. Mathematicians call this the ‘fundamental theorem of calculus’, because it says that the process of ‘integration’ is the inverse of ‘differentiation’.
In fact, the Babylonian representation of the total movement of Jupiter by means of an area illustrates this result very nicely. The speed of Jupiter across the sky can be measured by the number of units that it travels in one day, so that the numbers 3, 2, 2, 1, 2 represent the varying speed of the planet. Translating this idea into pictorial form gives us an illustration of the fundamental theorem.
So my suggestion is that the clay tablet describes a universal method of measuring a cumulative effect. This method was probably used in Babylon to assess the size of fields, and much later it was used by mathematicians to set up the subject we call integral calculus.