 Bernhard von Stengel, a Professor in LSE’s Department of Mathematics, uses his game theory knowledge to look into referendums, and considers how a referendum with more than two choices could be run…
Bernhard von Stengel, a Professor in LSE’s Department of Mathematics, uses his game theory knowledge to look into referendums, and considers how a referendum with more than two choices could be run…
Bernhard teaches discrete mathematics, optimisation and game theory at LSE. He is also on Twitter – @bvonstengel
If you favour a second referendum on Brexit (a prospect that is now, February 2019, receding), you should not only think of what you should ask the people, but how you would reconcile their choices. This is a central question of Mathematical Social Choice, with attempts to answer it since the middle ages (which is discussed in the ‘History’ section later in this post).
The question becomes interesting when there are more than two choices on the ballot paper. Suppose the choices are:
- D = leave the EU with a negotiated Deal (also called “soft Brexit”),
- N = leave the EU with No Deal (a “hard Brexit”), or
- R = Remain in the EU.
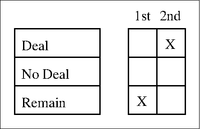
Every voter is given a first and second choice which represents their most and second-most preferred outcome. An example of a ballot is here:
On this ballot, the voter has expressed their choice as 1. R (Remain) and 2. D (Deal) with No Deal as the implicit third choice.
Assume we have 9 voters (or equal-sized voting groups) who have the following preferences:
Here, the first 4 columns are Remain voters whose preference is 1. Remain, 2. Deal, 3. No Deal. The next 3 columns are “Hard Brexiters” whose preference is exactly the reverse. The last 2 columns are voters whose first preference is Deal, with one of them having Remain as their second choice, the other No Deal as second choice.
These preferences and their distribution are not unrealistic.
A voting rule now tells us how to distill “the will of the people” from these preferences. But which rule should we choose? There are several contenders for such a rule.
Plurality, also called “First Past the Post”
This declares as winner the option that has gotten the most first-choice votes (so one does not even need a second choice and the ballot paper is simpler). In parliamentary elections in the UK, the MP representing a constituency is chosen in this way. Here the most first-choice votes (4 out of 9) are for Remain, but this is not a majority of all votes – 5 out of 9 would rather leave the EU without or with a deal.
Supplementary Vote, also called “Instant Runoff”
This means that the option that gets the least first votes is discarded, and the second preference of the voters who made that choice is counted (as if they would be asked to vote again in a “runoff” vote, assuming that the others stay with their first choice). Here, these are the voters who chose “D” and their votes are split, one of them for “R” and the second for “N”. The total is now 5 for Remain and 4 for No Deal, and Remain is the winner as the declared “will of the people” according to this rule.
The rule seems clear and fair enough, but it has its problems. The main problem is called strategic voting which means that voters have an incentive to mis-state their true preference. Namely, the minority (of people who chose “D”) now have in effect the casting choice between two polarised outcomes. If the above preferences were known (supported by opinion polls, say), then an “N” voter as above would have an incentive to mis-state their preference instead as 1=D 2=N 3=R (that is, swap their first and second choices), to let N become the decisive minority with 2 out of 9, after D which now has 3 out of 9 first choices. The other 2 N voters would both choose D and create the final vote 4 R versus 5 D, meaning to the leave the EU with a deal. While it remains doubtful that voters are that strategic, it would, on the other hand, create an incentive to be a bit more moderate.
However, not all voting rules favour R for the above voter preferences.
Condorcet winner, or pairwise comparison
This rule looks at the stated order of preferences and compares any two outcomes with each other. That is, the preferences of the voters are now used to answer a question such as “do you prefer D over N”?
Here we get the following answers:
- D beats R by 5 against 4 votes
- D beats N by 6 against 3 votes
- R beats N by 5 against 4 votes
This gives the following clear collective preference: a strict majority prefers D over R, and another strict majority prefers R over N, and another strict majority prefers D over N (which does not follow from the first two, see below). Here the “will of the people” is D first, R second, N third. Sounds great, but D was a first choice for only 2 out of 9 voters. Does this rule head for mediocre choices? Or for useful compromise?
The Condorcet rule has something less desirable than any of the other rules: It may not produce a clear winner but create cycles, as the following modified voter profile shows (three voters suffice):
Here, 2 thirds of voters prefer R over D, 2 thirds prefer D over N, and 2 thirds prefer N over R. Such voter preferences may not be realistic, but who knows? The fact that they are theoretically unavoidable for any reasonable voting system is known as “Arrows Impossibility Theorem”, after the economist Kenneth Arrow (1921-2017).
Borda count, or giving points
Yet another voting system tries to avoid cycles by giving points for first and second choice, for example 2 points for first choice, 1 point for second choice, 0 for third choice (instead of points 2,1,0 we could also give 3,2,1 with the same effect, which is just an extra point everywhere). The option with highest total number of points wins.
In our 9-voter example, this gives points
- R = 2+2+2+2+0+0+0+1+0 = 9
- N = 0+0+0+0+2+2+2+0+1 = 7
- D = 1+1+1+1+1+1+1+2+2 = 11
which makes again D the winner. But hey, what if someone does not put an “X” for their second choice at all? How should that shift the points? You get only one point for your first choice, and zero for the others? Or two points for your first choice, and zero for the others (which would surely let the Remain voters above drop their points for “D” in second place).
Or we could, like in football, give 3 points for first choice, 1 point for second choice, resulting in
- R = 3+3+3+3+0+0+0+1+0 = 13
- N = 0+0+0+0+3+3+3+0+1 = 10
- D = 1+1+1+1+1+1+1+3+3 = 13
with R and D tied. But why this rule?
Some history
The Condorcet method is named after the Marquis de Condorcet (1743-1794), who died in a prison cell, poisoned, during the French Revolution. However, it was already invented in 1299 by the Majorcan polymath Ramon Llull (ca. 1232-1316). To remember that name (which has 4 letters “L” in it and one vowel) think of the binary number 11011. Llull indeed invented the binary system and is considered by some as the inventor of information theory. He was so enthralled by it that he thought St Mary should be added to the Holy Trinity to make their number a power of two. Heretic stuff that did not make him popular with the church authorities. With the discovery in 2001 of his lost manuscripts, Ars notandi, Ars eleccionis, and Alia ars eleccionis, Llull is given credit for discovering the Borda count (re-discovered several times in later centuries) and the Condorcet criterion.
A very accessible book for general readers on these problems is Szpiro’s ‘Numbers Rule: The Vexing Mathematics of Democracy, from Plato to the Present’.
Conclusion
One conclusion is that you probably shouldn’t put more than two options on a ballot paper, or maybe not hold a referendum in the first place. On what voting system should you agree even to determine the “will of the people”, when we have enough trouble to determine it when they made one out of two choices? At any rate, you will appreciate “Strong Arrow’s Theorem” from the geeky cartoon XKCD (one of my favourites):
Can we ever agree on anything? Ask the mathematician!
You can watch Bernhard’s public lecture on ‘Game Theory and Politics’ here.


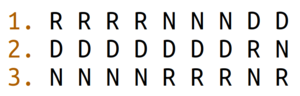
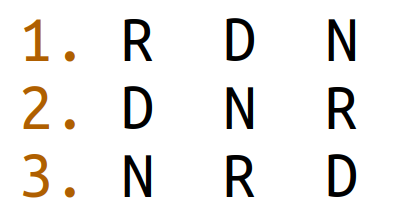



Interesting, but it is based on a dubious assumption that the three choices are on an equal footing.
They are not as the two, N and D, are sub-choices of the same choice: Brexit.
In order to avoid all these problems, why can’t we ask two questions:
1) Brexit or Remain?
2) should the result of the Q1 is Brexit, should we choose No Deal or (the May-EU) Deal?
None of those problems appear then.
George, the article was about voting systems. Anyhow, would you choose Brexit at any cost? Your proposal would not allow you to rank 1. D 2. R 3. N. Have you ever signed up for a deal without knowing its terms? No, of course not. Wait… If you voted for Brexit you did.
Already an excellent argument has been made at at https://blogs.sussex.ac.uk/uktpo/2018/12/17/organising-the-second-referendum/ that the two-step process should be “IF we leave the EU, then would you prefer May’s Deal or No Deal”, and once the option is clear,Already an excellent argument has been made at at https://blogs.sussex.ac.uk/uktpo/2018/12/17/organising-the-second-referendum/ that the two-step process should be “IF we leave the EU, then would you prefer May’s Deal or No Deal”, and once the option is clear, have a second referendum between this specific choice of leaving or staying in the EU.
As pointed out to me by Peter Sozou, this was done in New Zealand with changing their flag. They first chose a new design and then compared it to their old flag (which they kept). They did not first say “we hate the old flag”.
I came across the above discussion when my above blog entry was re-posted at https://blogs.lse.ac.uk/politicsandpolicy/a-mathematical-view-of-how-to-determine-the-will-of-the-people/
Already an excellent argument has been made at at https://blogs.sussex.ac.uk/uktpo/2018/12/17/organising-the-second-referendum/ that the two-step process should be “IF we leave the EU, then would you prefer May’s Deal or No Deal”, and once the option is clear, have a second referendum between this specific choice of leaving or staying in the EU.
As pointed out to me by Peter Sozou, this was done in New Zealand with changing their flag. They first chose a new design and then compared it to their old flag (which they kept). They did not first say “we hate the old flag”.