 Mathematician Bernhard von Stengel uses game theory to consider how a second Brexit referendum with more than two choices could be run, and how the counting-rule chosen for any multiple-choice ballot can determine the outcome.
Mathematician Bernhard von Stengel uses game theory to consider how a second Brexit referendum with more than two choices could be run, and how the counting-rule chosen for any multiple-choice ballot can determine the outcome.
If you favour a second referendum on Brexit (a prospect that is now, February 2019, receding), you should not only think of what you should ask the people, but how you would reconcile their choices. This is a central question of Mathematical Social Choice, with it attempts to answer since the middle ages. The question becomes interesting when there are more than two choices on the ballot paper. Suppose the choices are:
- D = leave the EU with a negotiated Deal (also called ‘soft Brexit’),
- N = leave the EU with No Deal (a ‘hard Brexit’), or
- R = Remain in the EU.
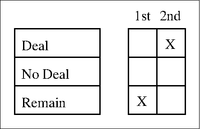
Every voter is given a first and second choice which represents their most and second-most preferred outcome. An example of a ballot is here:
On this ballot, the voter has expressed their choice as 1. R (Remain) and 2. D (Deal) with No Deal as the implicit third choice.
Assume we have 9 voters (or equal-sized voting groups) who have the following preferences:
Here, the first 4 columns are Remain voters whose preference is 1. Remain, 2. Deal, 3. No Deal. The next 3 columns are ‘Hard Brexiters’ whose preference is exactly the reverse. The last 2 columns are voters whose first preference is Deal, with one of them having Remain as their second choice, the other No Deal as second choice. These preferences and their distribution are not unrealistic. A voting rule now tells us how to distill ‘the will of the people’ from these preferences. But which rule should we choose? There are several contenders for such a rule.
Plurality, also called ‘first-past-the-post’
This declares as winner the option that has gotten the most first-choice votes (so one does not even need a second choice and the ballot paper is simpler). In parliamentary elections in the UK, the MP representing a constituency is chosen in this way. Here the most first-choice votes (four out of nine) are for Remain, but this is not a majority of all votes – five out of nine would rather leave the EU without or with a deal.
Supplementary vote, also called ‘Instant Runoff’
This means that the option that gets the least first votes is discarded, and the second preference of the voters who made that choice is counted (as if they would be asked to vote again in a ‘runoff’ vote, assuming that the others stay with their first choice). Here, these are the voters who chose ‘D’ and their votes are split, one of them for ‘R’ and the second for ‘N’. The total is now five for Remain and four for No Deal, and Remain is the winner as the declared ‘will of the people’ according to this rule.
The rule seems clear and fair enough, but it has its problems. The main problem is called strategic voting which means that voters have an incentive to mis-state their true preference. Namely, the minority (of people who chose ‘D’) now have in effect the casting choice between two polarised outcomes. If the above preferences were known (supported by opinion polls, say), then an ‘N’ voter as above would have an incentive to mis-state their preference instead as 1=D 2=N 3=R (that is, swap their first and second choices), to let N become the decisive minority with 2 out of 9, after D which now has three out of nine first choices. The other 2 N voters would both choose D and create the final vote 4 R versus 5 D, meaning to the leave the EU with a deal. While it remains doubtful that voters are that strategic, it would, on the other hand, create an incentive to be a bit more moderate. However, not all voting rules favour R for the above voter preferences.
Condorcet winner, or pairwise comparison
This rule looks at the stated order of preferences and compares any two outcomes with each other. That is, the preferences of the voters are now used to answer a question such as ‘do you prefer D over N’?
Here we get the following answers:
- D beats R by 5 against 4 votes
- D beats N by 6 against 3 votes
- R beats N by 5 against 4 votes
This gives the following clear collective preference: a strict majority prefers D over R, and another strict majority prefers R over N, and another strict majority prefers D over N (which does not follow from the first two, see below). Here the ‘will of the people’ is D first, R second, N third. Sounds great, but D was a first choice for only two out of nine voters. Does this rule head for mediocre choices? Or for useful compromise?
The Condorcet rule has something less desirable than any of the other rules: It may not produce a clear winner but create cycles, as the following modified voter profile shows (three voters suffice):
Here, two-thirds of voters prefer R over D, two-thirds prefer D over N, and two-thirds prefer N over R. Such voter preferences may not be realistic, but who knows? The fact that they are theoretically unavoidable for any reasonable voting system is known as ‘Arrows Impossibility Theorem’, after the economist Kenneth Arrow (1921–2017).
Borda count, or giving points
Yet another voting system tries to avoid cycles by giving points for first and second choice, for example two points for first choice, one point for second choice, zero for third choice (instead of points 2,1,0 we could also give 3,2,1 with the same effect, which is just an extra point everywhere). The option with highest total number of points wins.
In our 9-voter example, this gives points
- R = 2+2+2+2+0+0+0+1+0 = 9
- N = 0+0+0+0+2+2+2+0+1 = 7
- D = 1+1+1+1+1+1+1+2+2 = 11
which makes again D the winner. But hey, what if someone does not put an ‘X’ for their second choice at all? How should that shift the points? You get only one point for your first choice, and zero for the others? Or two points for your first choice, and zero for the others (which would surely let the Remain voters above drop their points for ‘D’ in second place).
Or we could, like in football, give 3 points for first choice, 1 point for second choice, resulting in
- R = 3+3+3+3+0+0+0+1+0 = 13
- N = 0+0+0+0+3+3+3+0+1 = 10
- D = 1+1+1+1+1+1+1+3+3 = 13
with R and D tied. But why this rule?
Some history
The Condorcet method is named after the Marquis de Condorcet (1743–1794), who died in a prison cell, poisoned, during the French Revolution. However, it was already invented in 1299 by the Majorcan polymath Ramon Llull (ca. 1232–1316). To remember that name (which has four letters ‘L’ in it and one vowel) think of the binary number 11011. Llull indeed invented the binary system and is considered by some as the inventor of information theory. He was so enthralled by it that he thought St Mary should be added to the Holy Trinity to make their number a power of two. Heretic stuff that did not make him popular with the church authorities. With the discovery in 2001 of his lost manuscripts, Ars notandi, Ars eleccionis, and Alia ars eleccionis, Llull is given credit for discovering the Borda count (re-discovered several times in later centuries) and the Condorcet criterion.
Conclusion
One conclusion is that you probably shouldn’t put more than two options on a ballot paper, or maybe not hold a referendum in the first place. On what voting system should you agree even to determine the ‘will of the people’, when we have enough trouble to determine it when they made one out of two choices? At any rate, you will appreciate ‘Strong Arrow’s Theorem’ from the geeky cartoon XKCD (one of my favourites):
___________________
The post was first published on LSE Department of Mathematics Research blog.
About the Author
 Bernhard von Stengel is a Professor of Mathematics at the London School of Economics. He teaches discrete mathematics, optimisation and game theory at LSE. He tweets as @bvonstengel.
Bernhard von Stengel is a Professor of Mathematics at the London School of Economics. He teaches discrete mathematics, optimisation and game theory at LSE. He tweets as @bvonstengel.


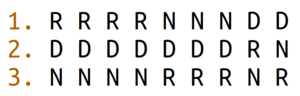
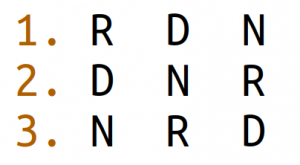







Sadly, the campaign to deny the result of the June 2016 referendum is supported by this article as well as the comments sofar. The proposal would invalidate the votes cast for Brexit, as simple as that, unless the choice1 is counted as valid without a choice made for choice 2. The by now old and dated canard that Leave does not indicate how Brexit is the be implemented should be retired. The referendum was very clear. Remainers have asked for a plan. The plan was clear, for the UK to LEAVE the EU. There is no mystery about a country being sovereign and independent. It has been tried before. Moreover, there are many countries doing it, and doing fine. The problem with Remoaners is that they will not give up, that they will not acknowledge that all the difficulties sofar about Brexit have nothing whatever to do with Brexit but are due to May’s government, or rather May in cooperation with the HoC, not preparing for Brexit but wasting time and threatening the country with full capitulation to the EU and vassal status. The aim is to deny the Brexit referendum result and shoehorn Remain back into play. It is a ploy directed from on high, supported by the mainstream media and seemingly supported by many remainers. It is unwise to undermine democracy thus, and if successful the fruits of this endeavour will leave a sour taste for generations.
I’m afraid that this discussion seems to miss the real points. First, there are only two strong grounds for holding another referendum: a) to resolve an unbreakable deadlock in Parliament – which is still to materialise as I write; b) to ‘ratify’ or ‘legitimise’ a decision by Parliament (call it May’s New Deal) which will still leave a substantial number of MPs and their constituents profoundly dissatisfied. None of the proposed ‘solutions’, however erudite, really deal with the logic of these reasons (though logic is not obviously of any substantial use in resolving the more primitive responses evident in the current debate and its ancestry).
The only ‘logical’ way of asking the population to either resolve a parliamentary deadlock or to provide any constituent legitimacy to their ‘solution’ is to recognise the importance of the sequencing of the issues:
1) Do you accept May’s New Deal? Yes or No;
2) Given that the answer to question 1 is no; should we: a) leave the EU anyway (i.e. without a deal); or (b) suspend or revoke A50 and stay as we are now?
Why not a two part vote, all on the same ballot
part one, Leave or remain
part two If leave were to win part one, chose deal as on table or no deal
One main problem is that “Leave the EU” is not well defined.
Even if you hate your current house, you don’t sell it
before you know where you would move to instead.
Michael Romberg below suggests to first decide what Brexit
would look like and then, with a specific alternative of
Leaving, vote on whether to Leave or Remain.
New Zealand did this with their new flag: First vote on a
new design, then whether to choose that or keep the old
flag. They did not say “we just hate the old flag”.
Rather than using polling data, every such article that I’ve read uses a test sample specifically chosen to highlight the potential contradictions that multiple voting presents. The fact that this new method is not perfect is then used either to back the first past the post system (even though it is much more flawed), or to support the original Brexit vote (even though the binary choice offered was an absolute disaster).
Those thought experiments are counterproductive, since the likely outcome is that most if not all of those methods would be aligned, and that we could set up rules to say that the referendum would be inconclusive if two chosen methods returned conflicting outcomes.
It is a bit narrow minded that on the basis that no method is perfect we should settle with the current system, ignoring the well known pros and cons of the various alternatives (https://en.wikipedia.org/wiki/Condorcet_method#Evaluation_by_criteria), which should allow us to have a serious debate about the best option.
Another method is to focus on the final question and work backwards from there.
In the end, if we leave the EU we would do so on just one of the many plans. So the final question is “Leave on this one plan, or Remain?”. That’s Round 2.
A prior voting round chooses the best of the Brexit options to go forward to the next round.
Economists call this “backward induction”. It is set out rather more elegantly than I have done in a blog by Professor Alan Winters of the UK Trade Policy Observatory:
https://blogs.sussex.ac.uk/uktpo/2018/12/17/organising-the-second-referendum/
“Another method is to focus on the final question and work backwards from there.” But what is the final question? You could equally well argue it for being “Do we revoke Article 50 or not”, if the first referendum has rejected the withdrawal deal. Or it could be “Do we revoke Article 50, or remain committed to a frictionless border via the withdrawal agreement” if the first referendum has rejected No Deal. This is certainly not a question you can settle mathematically. I’m not an economist so I don’t know whether it can be settled economically, but I doubt it. Since none of the three options (Remain, No Deal, Withdrawal agreement) enjoys a majority at the moment, I suppose most will want whichever option they most dislike to be eliminated by the first referendum.
Prof. von Stengel demonstrates clearly that 1 round of voting would be unsatisfactory. However, the 2 rounds proposed by Mr Romberg would require Remain voters to vote for the least worst (in their view) of the Brexit options in Round 1. Many may abstain, which would skew the voting. Subject to agreeing which Brexit options are put to the voters (additional ones could in theory include the ‘Norway’, the ‘Swiss’ and the ‘Canada’ options) – something which affects all voting schemes – the better approach seems to be the French one, where all options are put to the vote in Round 1, with a run-off between the top two in Round 2. There might be some merit in having second preferences in the first round, so the resulting top two options are seen to be clearly ahead of the others.