 Earlier this year on this blog, Fabrice Barthélémy, Mathieu Martin, and Ashley Piggins showed that under the Electoral College system, the arbitrary size of the House of Representatives, not the voters, can determine the outcome of a presidential election. They referred to work by Nicholas R. Miller to explain this ‘House size effect.’ Here he further explores the issue and writes that, even without ‘Senate’ electoral votes, the winner of the electoral vote could still depend on the size of the House.
Earlier this year on this blog, Fabrice Barthélémy, Mathieu Martin, and Ashley Piggins showed that under the Electoral College system, the arbitrary size of the House of Representatives, not the voters, can determine the outcome of a presidential election. They referred to work by Nicholas R. Miller to explain this ‘House size effect.’ Here he further explores the issue and writes that, even without ‘Senate’ electoral votes, the winner of the electoral vote could still depend on the size of the House.
In the language of Madison’s Federalist 39, the apportionment of electoral votes in Presidential elections is a compromise between the ‘federal’ principle of state equality embodied in the Senate and the ‘national’ principle of state representation according to population embodied in the House of Representatives. Given a fixed number of states, the weighting of the two principles is determined by the size of the House, which Congress can change by simple legislation (and did so regularly until about a hundred years ago). At present, and counting the District of Columbia as a state for electoral vote purposes, there are 102 ‘Senate’ electoral votes (two for each state) and 436 ‘House’ electoral votes (all others).
Typically the federal and national principles give the same verdict — that is, one candidate carries a majority of states and therefore wins a majority of Senate electoral votes and the same candidate wins a majority of House electoral votes. But the two principles sometimes give conflicting verdicts. For example, in the 2000 election Bush carried 30 states to Gore’s 21, giving Bush a margin of 18 with respect to Senate electoral votes, while Gore won 225 House electoral votes to 211 for Bush, giving Gore a margin of 14, so Bush won by an overall margin of four electoral votes. However, if the House size had been larger, Gore’s House electoral vote margin would have been increased in roughly the same proportion so, with a sufficiently larger House, Gore would have won an overall electoral vote majority.
This illustrates the House size effect: the winner of the election, i.e., the candidate who wins a majority of electoral votes, depends on the size of the House. The 2000 example suggests that a presidential election is subject to the House size effect if and only if (1) one candidate (say A) wins a majority of the Senate electoral votes, and (2) the other candidate (say B) wins a majority of the House electoral votes. The logic of the House size effect is suggested in Figure 1. (For the moment ignore the squiggly line overlying the smooth ‘Total EV% for Candidate A’ line.)
Figure 1 – Illustration of Conditions for the House Size Effect (EV= electoral votes)
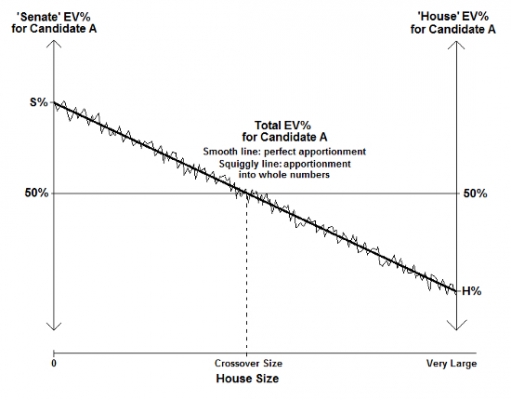
Note: Candidate A wins a majority (S% > 50%) of ‘Senate’ electoral votes but the states A carries collectively have less than half (H% < 50%) of the total population. House size runs from zero to very large and determines whether A wins a majority of the total electoral vote. The smooth line connecting S% and H% shows the percent of the total electoral vote won by A as a function of House size under perfect apportionment. The squiggly line fluctuating around the smooth line reflects ‘local chaos’ in apportionment and schematically indicates the percent of the total electoral vote won by A as a function of House size under actual (imperfect) apportionment.
As a summary of the historical record of presidential elections since 1828, this statement holds up without exception. Table 1 shows the five presidential elections, plus a counterfactual version of the 1860 election in which Lincoln faces a unified opposition, that meet these conditions.
Table 1 – Historical Presidential Elections Subject to the House Size Effect
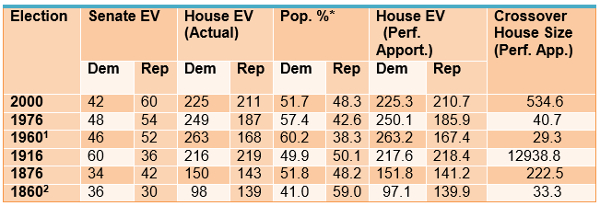
*Percent of population in states carried
1Kennedy is credited with carrying Alabama and winning all of its electoral votes; an unpledged elector slate carried Mississippi (8 electoral votes)
2 Counterfactual two-candidate election: Lincoln vs. united opposition
But as a theoretical proposition, the statement above does not (quite) hold up. This is because the apportionment of House seats is an unavoidably quirky matter, given that relatively small whole numbers of seats cannot be apportioned among the states in a way that is perfectly proportional to much their much larger populations. This implies that whether a candidate wins a majority of House electoral votes may itself depend on the size of the House.
We can sidestep the apportionment problem by supposing that the House of Representatives is (hypothetically) perfectly apportioned by assigning each state a quota of House seats that is perfectly proportional to its population and as such is almost never a whole number. (Under perfect apportionment Gore would have won 225.3 and Bush 210.7 House electoral votes in 2000.)
If the House were perfectly apportioned, a Presidential election would be subject to the House size effect if and only if (1) one candidate (say A) carries a majority of states, and (2) the other candidate (say B) carries states that collectively hold a majority of the total population.
Furthermore, the crossover House size at which candidate A’s margin with respect to Senate electoral votes is precisely balanced by candidate B’s margin with respect to perfectly apportioned House electoral votes (thereby producing an electoral vote tie) is given by A’s margin with respect to Senate electoral votes divided by the B’s margin with respect to the percent of population of states carried. Thus in 2000 Bush won 30 states to Gore’s 21 and Gore carried states with 51.6834 percent of the apportionment population to Bush’s 48.3166 percent, so perfect apportionment implies a crossover House size of (60 − 42) / (0.516834 − 0.483166) ≃ 534.64.
But since House seats are not, and cannot be, perfectly apportioned among the states, we must confront the apportionment problem. There are many different apportionment methods, four of which have actually been used to apportion House seats, which may produce (slightly) different allocations of House seats for a given House size and profile of state populations.
Whatever the method, candidate B’s margin with respect to House electoral votes generally increases with House size, but this margin does not and cannot increase in a smooth fashion. Suppose that the House is a given size and is then increased by one seat. The additional seat will be awarded to the state with the strongest claim to it (according to the apportionment method in use) but that state may well have been carried by A, in which event B’s electoral vote margin decreases rather than increases. In general, the relationship between House size and candidate B’s House (and total) electoral vote margin is ‘locally chaotic,’ as documented by the data from 2000 shown in Figure 2 (adapted from calculations by Michael G. Neubauer and Joel Zeitlin) and schematically suggested by the squiggly overlay around the smooth ‘Total EV%’ line in Figure 1.
Figure 2 – Actual ‘Local Chaos’ in 2000 Election
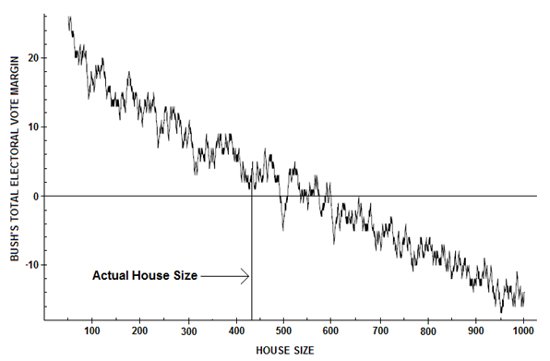
Source: Adapted from Graph 1 in Michael G. Neubauer, and Joel Zeitlin, ‘Outcomes of Presidential Elections and the House Size.’ PS: Political Science and Politics, 36/4 (2003): 721-725.
When we take account of the ‘locally chaotic’ effects of apportionment, the previously stated conditions remain sufficient for the House size effect but are no longer (quite) necessary. This becomes evident if we consider how Figure 1 would look if condition (1) were not met and S% fell just below the 50% mark; while candidate B would win at almost all House sizes, ‘local chaos’ might give candidate A just over half of the House and total electoral vote at some small House sizes, so there would still be a House size effect. (In somewhat similar fashion, Table 1 shows that the Democrat, Samuel Tilden, was ‘candidate B’ in 1876, generally benefitting from a larger House size. But even with an actual House size considerably larger than the crossover size, Tilden lost because of ‘local chaos.’)
Indeed, suppose the Electoral College were modified by abolishing ‘Senate’ electoral votes entirely. Given perfect apportionment of House electoral votes, candidate A’s percent of the electoral vote would be the constant function EV% = H%; but, given any actual apportionment of House seats (and electoral votes) into whole numbers, ‘local chaos’ would still produce a squiggly overlay around this horizontal line so, if H% were very close to the 50% mark, the electoral vote winner could still vary with House size.
This fact has interesting implications in another electoral context: parliamentary elections held under list proportional representation. Here political parties are the counterpart of states, being apportioned seats on the basis of their electoral support, and coalitions of parties are analogous to the ‘coalitions’ of states that support presidential candidates. If two complementary coalitions of parties each receive very close to 50% of the vote, their majority vs. minority status with respect to parliamentary seats could vary with the size of parliament. (For examples of such inversions, see here.)
This article is based on the paper “The House Size Effect and the Referendum Paradox in U.S. Presidential Elections”, Electoral Studies, 35 (September 2014): 265-271. An ungated version is available here.
Featured image credit: Mike McCune (Flickr, CC-BY-2.0)
Please read our comments policy before commenting.
Note: This article gives the views of the author, and not the position of USApp– American Politics and Policy, nor of the London School of Economics.
Shortened URL for this post: http://bit.ly/1tw6emu
_________________________________
 Nicholas R. Miller – University of Maryland Baltimore County
Nicholas R. Miller – University of Maryland Baltimore County
Nicholas R. Miller is Research Professor of Political Science at the University of Maryland Baltimore County (UMBC). His research interests lie in the area of formal political theory and social choice, especially voting processes and spatial voting models, and the U.S. Electoral College. He is author of a monograph on Committees, Agendas, and Voting and is co-editor of the forthcoming Elgar Handbook of Social Choice and Voting. He is a past editor of the Journal of Theoretical Politics and a past president of the Public Choice Society.




It’s going to take me a while to fully digest this article, but my first impression is that this so-called House Effect is of little practical significance. I also dispute some of the author’s underlying terminology. There is really no such thing as House or Senate electoral votes, there are just electoral votes period, divided up any way the legislatures of the respective states decide. True, the number of votes for each state is determined by each state’s total number of Senators plus Representatives, but beyond that there is no way to tie individual electors to any particular legislative seat, unless the state establishes such a relationship, as has been done in Nebraska and Maine only. Yes, Congress can legislatively change the total number of Representatives in the House, but they have not done so for more than 100 years, and in fact under 1929 legislation, the number has been capped at 435 (although that number could be legislatively changed). But as long as we are talking about once-a-century minutiae, shouldn’t we also worry about a Senate Effect – – – as in the (rare) case when a new state is admitted to the Union and is awarded two shiney new Senators plus their new Representatives? I love mathematical puzzles, but I think truly serious study of the electoral college will entail far more than this supposed House Effect the author postulates.