
 To reach perfect income equality, factors that determine individual income, such as intelligence, inherited wealth, personalities, and social skills, should be identical for everyone. That is an infeasible ideal. Chae Un Kim and Ji-Won Park propose a more feasible and realistic concept of income equality that could be incorporated in the Gini coefficient, the most widely used measure of inequality, guaranteeing the maximisation of overall social welfare without hampering overall economic efficacy.
To reach perfect income equality, factors that determine individual income, such as intelligence, inherited wealth, personalities, and social skills, should be identical for everyone. That is an infeasible ideal. Chae Un Kim and Ji-Won Park propose a more feasible and realistic concept of income equality that could be incorporated in the Gini coefficient, the most widely used measure of inequality, guaranteeing the maximisation of overall social welfare without hampering overall economic efficacy.
Income inequality is well known to negatively affect any economic system, and it has been the subject of political dispute for the past 100 years or more. Many methods have been proposed to measure income inequality quantitatively; of these, the Gini coefficient—which ranges from 0 (perfect equality) to 1 (perfect inequality)—is the most widely used measure. Perfect equality is achieved when all members of a given nation or society share the same income level. It’s often alleged within political disputes that perfect equality leads to economic inefficacy, and thus to a less productive society. Perfect income equality can only be achieved when everyone is identical and equally able to contribute economically. To reach perfect income equality, factors that determine individual income, such as intelligence, inherited wealth, personalities, and social skills, should be identical for everyone. However, these conditions cannot be met, even in the Smurfs’ village. Therefore, it’s obvious that the concept of perfect income equality is rather idealistic and practically infeasible in the real world.
If a more feasible and realistic concept of income equality can be incorporated in the Gini coefficient, it can provide a useful guideline for realistic and practical income distribution, guaranteeing the maximization of overall social welfare without hampering overall economic efficacy.
Figure 1 shows the Lorenz curve for a typical nation. The Lorenz curve illustrates the national income distribution (to the right of the perfect equality line). The perfect equality line cannot be a useful reference for the real world, so we need a more practical and feasible equality line. If it exists, this line provides a valuable reference for government policies (e.g., income taxes) for redistributing incomes and reducing income inequality.
Figure 1 – The Lorenz curve of a typical nation
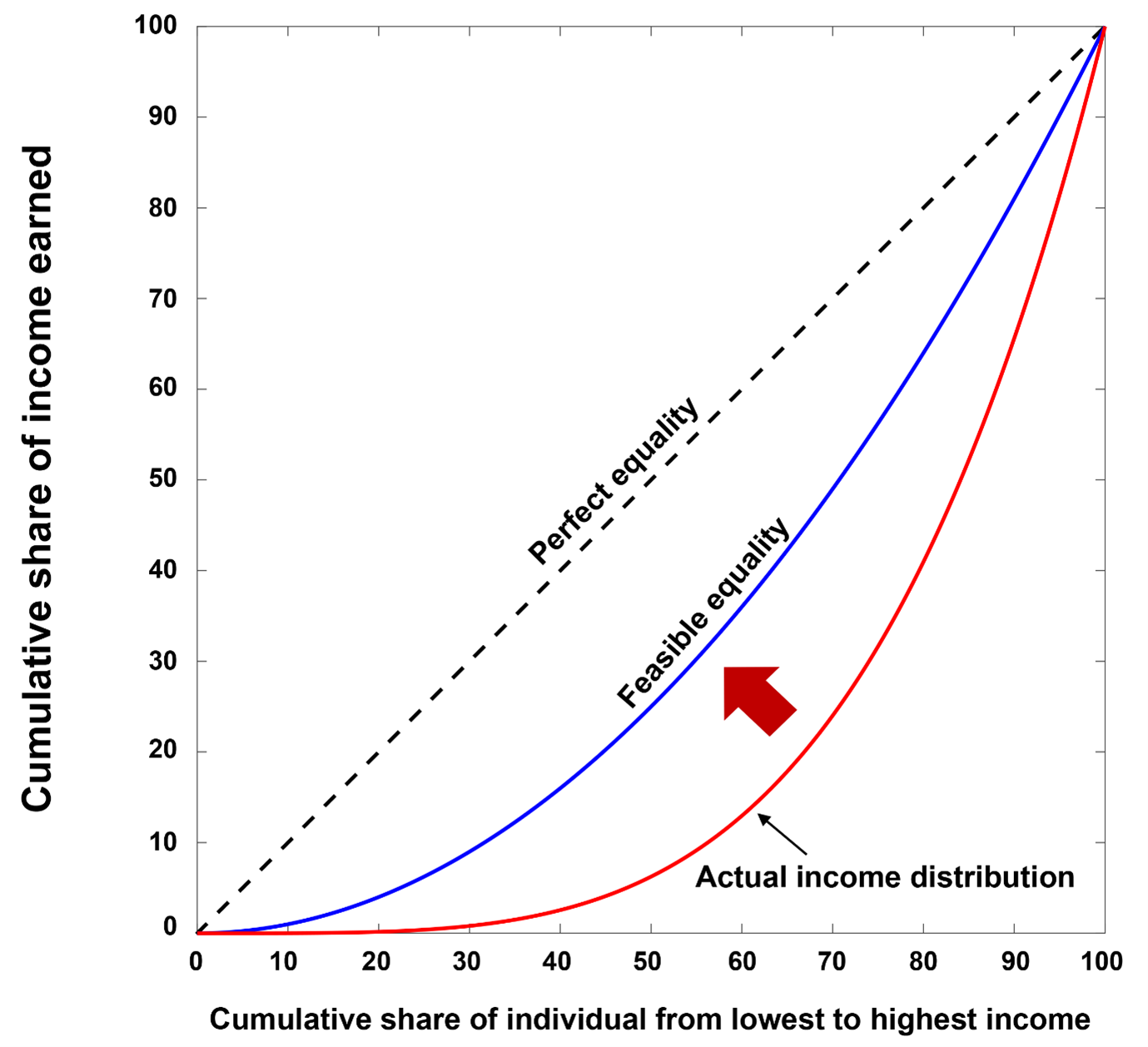
Feasible income equality is defined as an optimal income distribution that maximizes total social welfare without hindering the sustainable economic growth of a given nation or society. In addition, under a feasible income equality, income must be distributed fairly to individuals by properly reflecting the realistic factors influencing their economic contributions. In our study, an optimal income distribution (i.e., the feasible equality) could be modelled using the sigmoid welfare function and the Boltzmann income distribution. A sigmoid function is an S-shaped, non-linear function and is used in a wide range of research fields such as physics and economics. The Boltzmann income distribution is adapted from the physical sciences, where the underlying principle is based on entropy maximization and provides the most probable, natural, and unbiased distribution of a physical system at thermal equilibrium. The concept of most probable in the physical sciences was translated into fair in our study.
Figure 2 – Individual welfare function and total social welfare 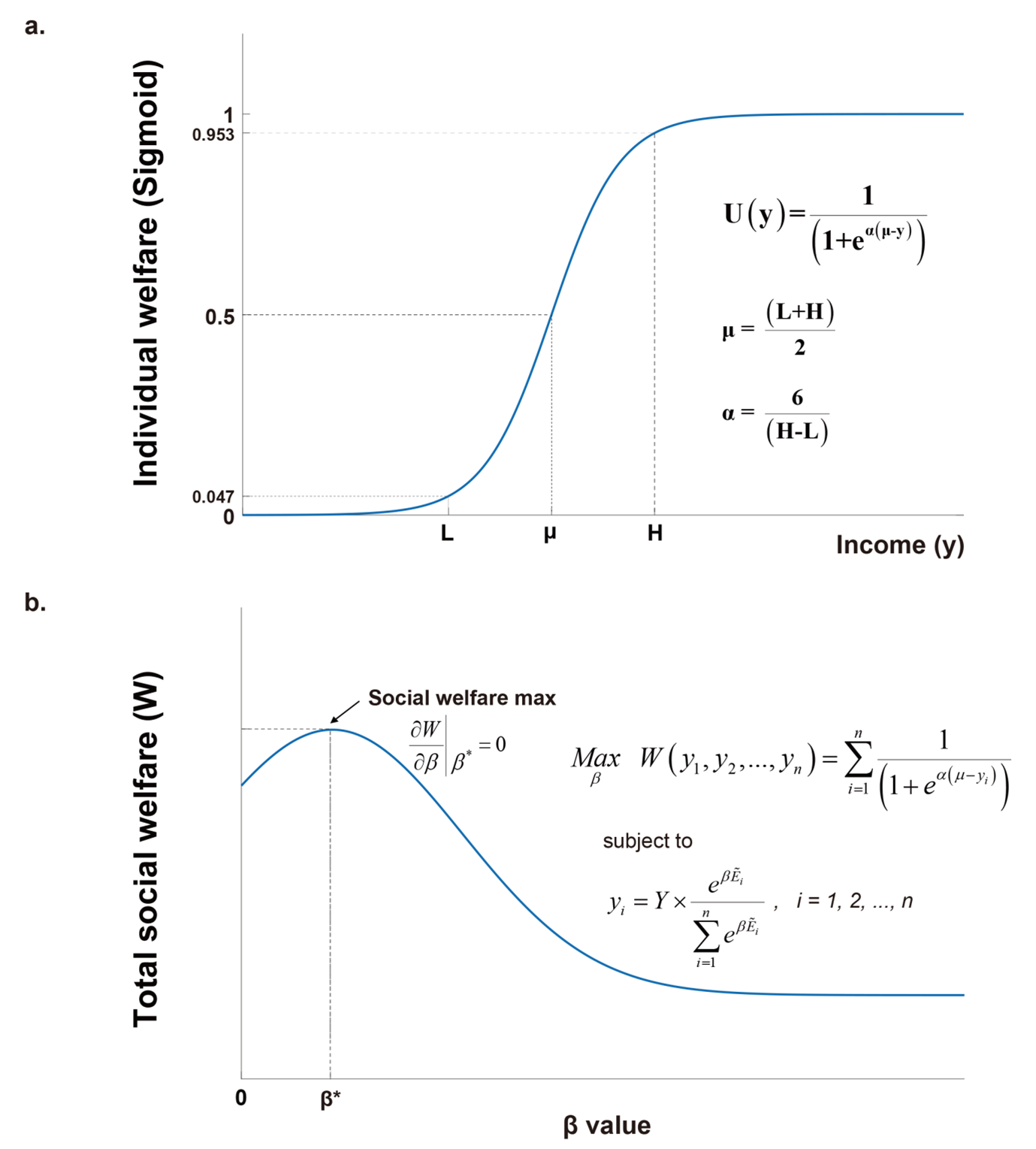 Notes: a) The non-linear sigmoid function, reflecting more realistic individual welfare as income increases. With the critical low- and high-income values (L and H), the two constants (µ and α) in the sigmoid function can be determined. b) The total social welfare function is maximized at β = β* (the optimal income distribution).
Notes: a) The non-linear sigmoid function, reflecting more realistic individual welfare as income increases. With the critical low- and high-income values (L and H), the two constants (µ and α) in the sigmoid function can be determined. b) The total social welfare function is maximized at β = β* (the optimal income distribution).
As shown in Figure 2-a, the sigmoid individual welfare function represents the realistic welfare, such as well-being, happiness, and satisfaction, that a person feels as their income increases. If their income is close to zero, welfare value must be at the minimum. Welfare value will increase as income rises, but not rapidly below the critical low-income value (i.e., the minimum cost of living). Because in this case income is still insufficient to support a basic living standard, welfare value increases slowly and gradually. But if income rises above the critical low-income value, people begin to experience some economic freedom. Hence, welfare value will suddenly increase rapidly. As income rises further, the degrees of economic freedoms increase and become saturated at a critical large sufficient income value. At the critical large-income value, the welfare value would also be saturated; afterward, welfare value would again increase only gradually.
As shown in Figure 2-b, the Boltzmann income distribution (Pi) is expressed as an exponential function of the income distribution factor (Ẽi), which is a measure of economic contributions and depends on factors such as intelligence, personality, and physical and social skills. According to the single value (β) in the Boltzmann distribution, the income distribution can represent a wide range of income distributions, from perfect equality (β = 0) to perfect inequality (β = ∞). When the Boltzmann income distribution is inserted into the sigmoid welfare function, the total social welfare function becomes a function of the β value and can be maximized at β*. The Boltzmann income distribution with β* represents the feasible equality (the optimal income distribution).
Based on the model, we conducted an empirical analysis of four countries (the US, China, Finland, and South Africa) and demonstrated how optimal income distributions could be evaluated. Figure 3 shows the Lorenz curves for the actual and optimal income distributions for each of those countries. In all countries, the Lorenz curves for actual income distribution are widely dispersed. By contrast, the Lorenz curve for optimal income distribution (the feasible income equality line) lies between the diagonal (idealistic perfect equal) and actual income lines. In addition, the shape of the feasible equality line is very similar for all four countries. This observation is supported by the Gini coefficient calculations. The Gini coefficients for the actual income distributions are relatively broadly distributed, whereas those for optimal income distributions are distributed narrowly. Therefore, this result raises the possibility that a universal feasible equality line could be found and applicable to all countries around the world.
Figure 3 – Lorenz curves for the actual and the optimal income distributions for four countries
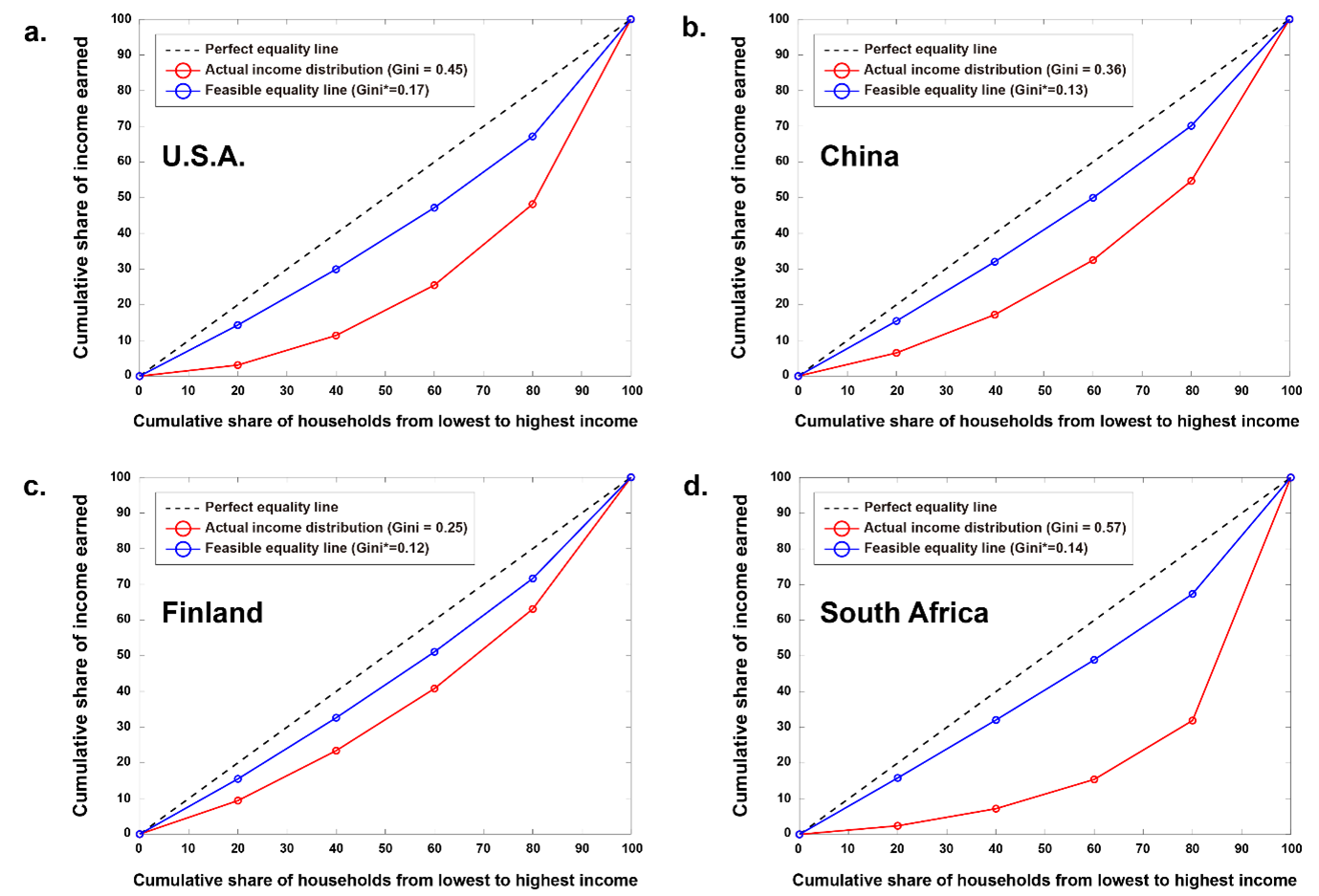
Note: The feasible equality lines (blue) are similar for all four countries. The hypothetical feasible equality line (blue) can serve as a practical guideline for government policies and interventions (red arrow).
In conclusion, our results show that the feasible income equality could provide a practical guideline for government policies (e.g., income taxes) and interventions for the redistribution of income and wealth. We strongly believe that our work provides direct input for future theoretical and empirical studies on reducing income inequality or suggesting government policies, and we anticipate opening a new window to feasible equality in the real world.
- This blog post is based on Getting to a feasible income equality, PLoS ONE 16(3): e0249204 (2021), and first appeared at LSE Business Review.
- Featured image by Thomas de LUZE on Unsplash
Please read our comments policy before commenting
Note: The post gives the views of its authors, not the position USAPP– American Politics and Policy, nor of the London School of Economics.
Shortened URL for this post: https://bit.ly/3gz8b3t
About the authors
 Chae Un Kim – Ulsan National Institute of Science and Technology
Chae Un Kim – Ulsan National Institute of Science and Technology
Chae Un Kim is an associate professor in the Department of Physics at UNIST (Ulsan National Institute of Science and Technology) in South Korea.
 Ji-Won Park – Cornell University
Ji-Won Park – Cornell University
Ji-Won Park is a Ph.D. recipient in regional science at Cornell University.



