 (No name) by Pixapopz, under a CC0 licence
(No name) by Pixapopz, under a CC0 licence
Although the college gender gap has reversed, females are still under-represented in high-powered and high-paid careers as CEOs, Ph.D.s, and more generally in finance, business, science, technology, engineering, and maths (STEM) fields.
In a recent paper (Joensen and Nielsen, 2016), we assess three potential explanations for this inequality. First, are the labour market rewards for advanced maths skills lower for females than for males? Second, are females less talented than males in terms of maths abilities? Third, does the way we market and teach maths in schools drive talented females away? The answers to the questions are: no, no, and yes! In particular, we show that restrictive course bundling in high school constitute a barrier for female maths talents.
Why have these questions not already been answered? Gender differences in maths qualifications may explain a substantial part of the gender gap in income and in career outcomes, because the positive causal effect of advanced maths on earnings is sizeable (Altonji, 1995; Rose and Betts 2004; Joensen and Nielsen, 2009). Several studies (Paglin and Rufolo, 1990; Rose and Betts 2004; Goldin, Katz and Kuziemko, 2006; Altonji, Blom and Meghir, 2012) touch upon the link between lack of female maths qualifications and the gender wage gap. Goldin et al. (2006) also argue that better female college preparedness, including completion of advanced maths and science courses in high school, is an important factor in the reversal from male-dominated colleges to female-dominated colleges in the US. But causality is still not established due to the lack of variation in the choice of maths that is random with respect to unobservable factors affecting both the choice of maths, subsequent career choices, and income. Such unobservable factors include maths ability and motivation.
How do we answer these questions? We analyse Danish administrative data for three cohorts of high school students whose education and labour market careers have been followed for 21 years after they started high school in 1984-86. The study is based on a pilot scheme that unexpectedly and randomly allowed for a more flexible combination of advanced maths with other courses. Advanced maths teaches the students more advanced algebra and geometry compared to intermediate high school maths. Advanced maths is a prerequisite to enter most STEM fields in college. In the traditional high school, advanced maths could only be combined with advanced physics, but the pilot scheme also offered the option to combine advanced maths with chemistry. This was a minor change in choice sets, since it simply swapped advanced for intermediate chemistry and intermediate for advanced physics compared to the traditional advanced maths course option. But this additional option had a substantial impact on the choices of students at schools that adopted the pilot scheme. Only one out of ten girls chose advanced maths before the pilot scheme, but this fraction doubled after it was introduced. The fraction also increased for boys: from four out of ten to half choosing maths.
Maths also boosts income for females
Girls at the top and boys at the middle of the maths-ability distribution took more maths because of the cost reduction. These advanced maths qualifications provided the basis for more successful careers: 30 per cent higher earnings on average. The average earnings gains were at least as high for females as for males.
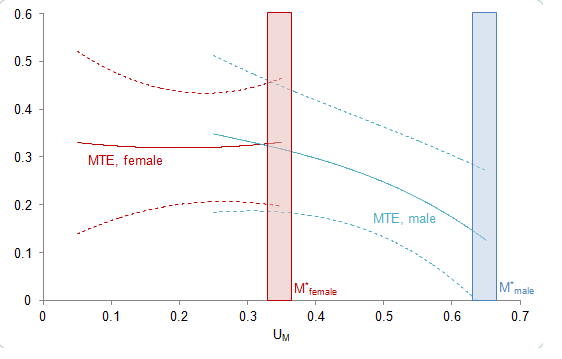
Figure 1. Causal effect of maths on earnings, marginal students
Note: The figure is equivalent to Figure 3 in Joensen and Nielsen (2016) which we refer to for a detailed description. The horizontal axis displays the probability to choose advanced maths in high school. This is the unobserved cost relative to unobserved gain of advanced maths that we label maths ability. The vertical axis displays the causal effect of advanced maths on earnings 12-21 years after high school entry with solid lines (incl. 95 per cent confidence intervals with fine dashed lines). The dark red lines display the female figures, while the light blue lines display the male figures. The shaded bars highlight those who would be at the margin of choosing advanced maths if costs were reduced even further.
For girls and boys with identical abilities, the earnings gains from studying maths are equal. While we refer Joensen and Nielsen (2016) for detailed explanations, this can be seen by the overlapping red and blue lines in Figure 1, which illustrates the earnings gains caused by advanced maths across the ability distribution. The fact that earnings gains are equal across gender for individuals with an identical ability indicates that there is no gender discrimination in the labour market as to rewarding individuals with similar maths ability equally for their advanced maths qualifications. This also indicates that the underlying maths ability distribution is equal, at least around the top decile of the distribution.
What if costs were to be reduced even more? The students who would be at the margin of choosing maths if costs were reduced further are highlighted by the shaded areas in Figure 1. The figure reveals that the earnings benefits to the marginal girls are substantial when only 20 per cent of them take maths, whereas the benefits to the marginal boys are not significantly different from zero when half of them already take maths. This means that there is a considerable fraction of girls who would gain from choosing maths when only the girls of highest ability choose maths, while boys of more mediocre ability also choose maths. There is indeed ample unexploited maths talent among girls to be retrieved. Our results suggest that this maths talent can be retrieved by allowing for even more flexible bundling of courses in high school curricula. For example, allowing advanced maths to be bundled with other advanced science courses that appeal more to girls.
How and why does maths boost income?
We also analyse how advanced maths qualifications affect the position in the earnings distribution. We find that maths moves females to the top of the earnings distribution, while it prevents males from falling to the bottom of the earnings distribution. Overall the impacts across the maths ability distribution and the earnings distribution suggest that advanced maths pushes high ability students to the top of the earnings distribution, while it pulls more mediocre maths-ability students from the bottom and does not have a significant impact on low maths-ability students.
Why is there such a large income boost by studying advanced maths for high ability females? We find that they end up performing better in the education system, because it makes more of them complete Master’s and PhD degrees instead of 2- and 4- year college degrees. However, the fact that advanced maths makes females drift away from traditional female education in the humanities towards high-paid education in health sciences and technical sciences also indicates that preferences, self-confidence, or self-perception may be affected by succeeding with advanced maths in high school. We even find that they become more likely to work in more competitive career tracks in the private sector and to become CEOs.
The high earnings gains thus encompass that high-ability females switch towards more advanced and more maths-intensive college fields, pursue more competitive career tracks, and subsequently climb higher up in the earnings distribution and to some extent also the corporate hierarchical ladder.
How to identify, attract, and foster talent?
We believe that our conclusions generalise to populations where substantially more males than females choose the most maths-intensive college majors and careers. This includes most Western European countries and the US. Many studies hint at cultural differences across countries, across education systems and across individual schools as important explanations for the gender gap in maths qualifications (Andreescu et al. 2008; Guiso et al., 2008; Bedard and Cho, 2010; Ellison and Swanson, 2010; Fryer and Levitt, 2010; Pope and Sydnor, 2010). Therefore, it seems obvious that there is scope for improving female maths qualifications and subsequent career outcomes by understanding why and how educational environments affect the costs of achieving maths qualifications: How is maths taught? How is maths marketed? And – in our case – how is maths bundled with other courses?
Our results suggest that neither lack of abilities nor labour market rewards discourage girls from taking advanced maths courses. Instead it seems that access is deterred by too restrictive bundling of courses. This suggests there is a lost pool of maths talent among high-ability girls that may be accessed by changing the costs embedded in the educational environment and the institutional set-up of maths teaching. This may even be beneficial for the economy as a whole as identifying, attracting, and fostering the most talented people to succeed in STEM careers could increase innovation, productivity, and economic growth.
Why do talented females shy away from advanced maths – despite the economic benefits being so high? Our recent paper (Joensen and Nielsen, 2016) provides hard evidence on one aspect of cost in the educational environment, which may be a barrier to attract the most talented people to achieve their maximum potential. It also highlights that much more research is needed on how to identify, attract, and foster this lost pool of talent.
♣♣♣
Notes:
- This blog post is based on the authors’ paper Mathematics and Gender: Heterogeneity in Causes and Consequences, The Economic Journal, June 2016.
- The post gives the views of its authors, not the position of LSE Business Review, the London School of Economics or the University of Minnesota.
- Before commenting, please read our Comment Policy
 Juanna Schrøter Joensen is a Senior Research Associate at the Department of Economics at the University of Chicago, a network member of the Human Capital and Economic Opportunity (HCEO) Global Working Group, and a research fellow in the Institute for the Study of Labor (IZA). Her research focuses on understanding the causes and consequences of individual human capital investments. It highlights important aspects of heterogeneity in human capital investments and its interaction with institutions and public policies; such as curricula, grading, and study aid schemes. Her PhD dissertation was prized the best in Social Sciences in 2007 and the best in Economics in the two-year period 2006-2007 at Aarhus University. She also received the European Association of Labour Economists (EALE) Young Labour Economist Prize 2009. Email: jjoensen@uchicago.edu
Juanna Schrøter Joensen is a Senior Research Associate at the Department of Economics at the University of Chicago, a network member of the Human Capital and Economic Opportunity (HCEO) Global Working Group, and a research fellow in the Institute for the Study of Labor (IZA). Her research focuses on understanding the causes and consequences of individual human capital investments. It highlights important aspects of heterogeneity in human capital investments and its interaction with institutions and public policies; such as curricula, grading, and study aid schemes. Her PhD dissertation was prized the best in Social Sciences in 2007 and the best in Economics in the two-year period 2006-2007 at Aarhus University. She also received the European Association of Labour Economists (EALE) Young Labour Economist Prize 2009. Email: jjoensen@uchicago.edu

Helena Skyt Nielsen is a professor of Economics, Aarhus University, and she earned her PhD in Economics from Aarhus University in 1999. Her research primarily concerns education and family economics, and her current projects study family dynamics and school resources among other things. She has published more than forty academic articles in leading international journals. She is a member of the Danish Council for Independent Research | Social Sciences. She is a research fellow at the Institute for the Study of Labor (IZA) in Bonn, Germany, and an affiliate with TrygFondens Centre for Child Research. She serves as an editor-in-chief of Labour Economics. Email: hnielsen@econ.au.dk