To maximise revenue from an auction, an important question is how to design it. A combinatorial auction is one where bids are allowed not only on individual items, but on combinations of items, called packages, as well. The auctioneer aims to accept the bids that together maximise revenue. This is called the winner determination problem — a mathematical problem. As the number of items in an auction increases, the number of steps required to design the optimal combination increases exponentially, and so does the time required to solve the puzzle. Together with his colleague Frank Kelly, Richard Steinberg developed a combinatorial auction procedure called PAUSE (Progressive Adaptive User Selection Environment) in which the auctioneer never faces the winner determination problem.
In many auctions, an item’s value to a bidder increases if another item, or group of items, is also won by that bidder. For example, six chairs and a table offered individually at auction might fetch £100 for each chair and £200 for the table, yielding £800 in revenue:
Figure A. Items offered individually at auction

However, these seven items might fetch more, perhaps £1000, if offered as a complete set:
Figure B. Items offered as a complete set at auction

This ‘synergistic’ effect can be bidder-specific, i.e., a desirable set for you might not be a desirable set for others. Thus, the auctioneer might not know how to group items in advance.
Therefore, auctioneers have an incentive to allow bids on combinations of items, resulting in more bidding and higher bids, and thus higher revenue, and no bidder will get stuck paying for an incomplete set of items. A combinatorial auction is one where bids are allowed not only on individual items, but on combinations of items—called packages—as well.
The “standard approach” to running a combinatorial auction is to ask bidders in each round to submit their individual bids and package bids. The auctioneer then accepts those bids that together maximise his revenue. This winner determination problem is, unfortunately, in a class of mathematical problems called NP-hard. This means that, as the size of the problem (e.g., number of items in an auction) increases, the number of steps required to solve the problem increases exponentially, and thus the time required to solve the problem increases enormously.
The PAUSE auction
Cambridge professor Frank Kelly and I developed a combinatorial auction procedure called PAUSE (Progressive Adaptive User Selection Environment) where the auctioneer never faces the winner determination problem. PAUSE proceeds in stages. In stage 1, bidders submit bids on individual items only. In stage 2, bidders can submit package bids that contain two items. However, each bidder must submit his package bid as part of a composite bid, which is a set of non-overlapping bids that cover all the items in the auction. Of course, a bidder is unlikely to be interested in all the items in the auction; however, he can fill out his composite bid with previously submitted bids by any of the bidders. In stage 3, bidders can submit package bids with up to three items; in stage 4, up to four items, and so forth, as long as the bids are submitted as part of a composite bid. Each stage can have several rounds of bidding.
The PAUSE procedure is illustrated below. Figure 1 shows six items to be auctioned—think of them as six adjoining parcels of land—and four bidders: blue, red, yellow, and green.
Figure 1. The six items and the four bidders

Figure 2 shows the final round of stage 1. The six items had been auctioned off in six simultaneous auctions, with Blue provisionally winning the two items on the left at prices 1 and 3; Red, the two items at the top-middle and top-right at prices 3 and 2; and Yellow, the two items on the bottom-middle and bottom-right at prices 2 and 5. Green is not a provisional winner on any item.
Figure 2. The stage 1 bids
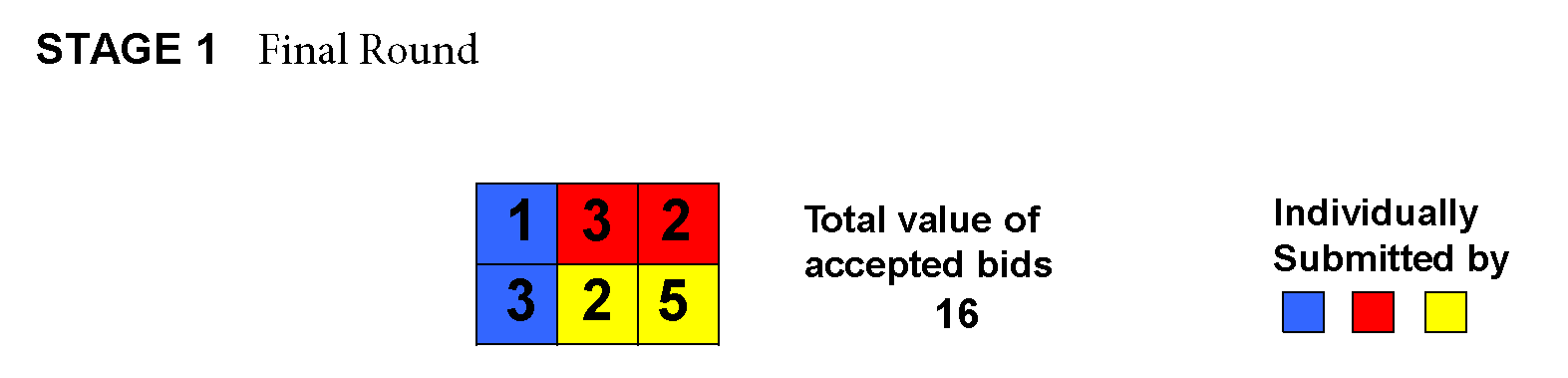
Figure 3 shows the composite bids submitted in stage 2, round 1.
Figure 3. Proposed bids in stage 2, round 1
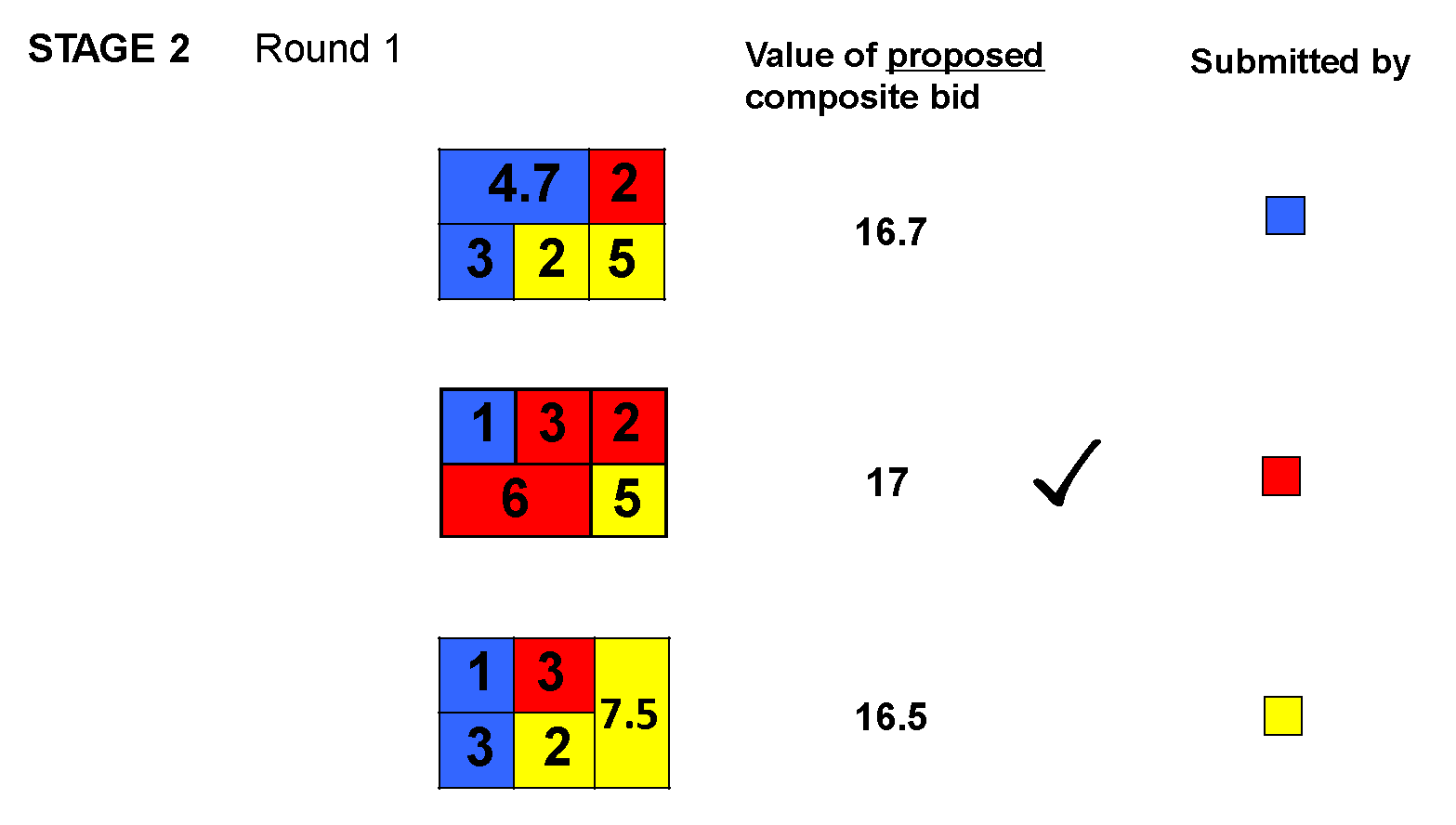
Here, Blue, Red, and Yellow have each submitted a composite bid, while Green has decided to stay out of the bidding for now. Blue’s composite bid has improved on adjacent bids from stage 1 of 1 from himself and 3 from Red with a package bid of 4.7, and he has filled out the remainder with bids from stage 1, for a composite bid of 16.7. Red has submitted a composite bid of 17, and Yellow a composite bid of 16.5. Thus, Red’s composite bid of 17 is highest and thus is the one accepted in round 1 of stage 2.
Figure 4 shows the accepted composite bids in each of three rounds of stage 2. (For simplicity, the losing composite bids in each round are not shown.)
Figure 4. Accepted composite bids in stage 2, rounds 1, 2, and 3
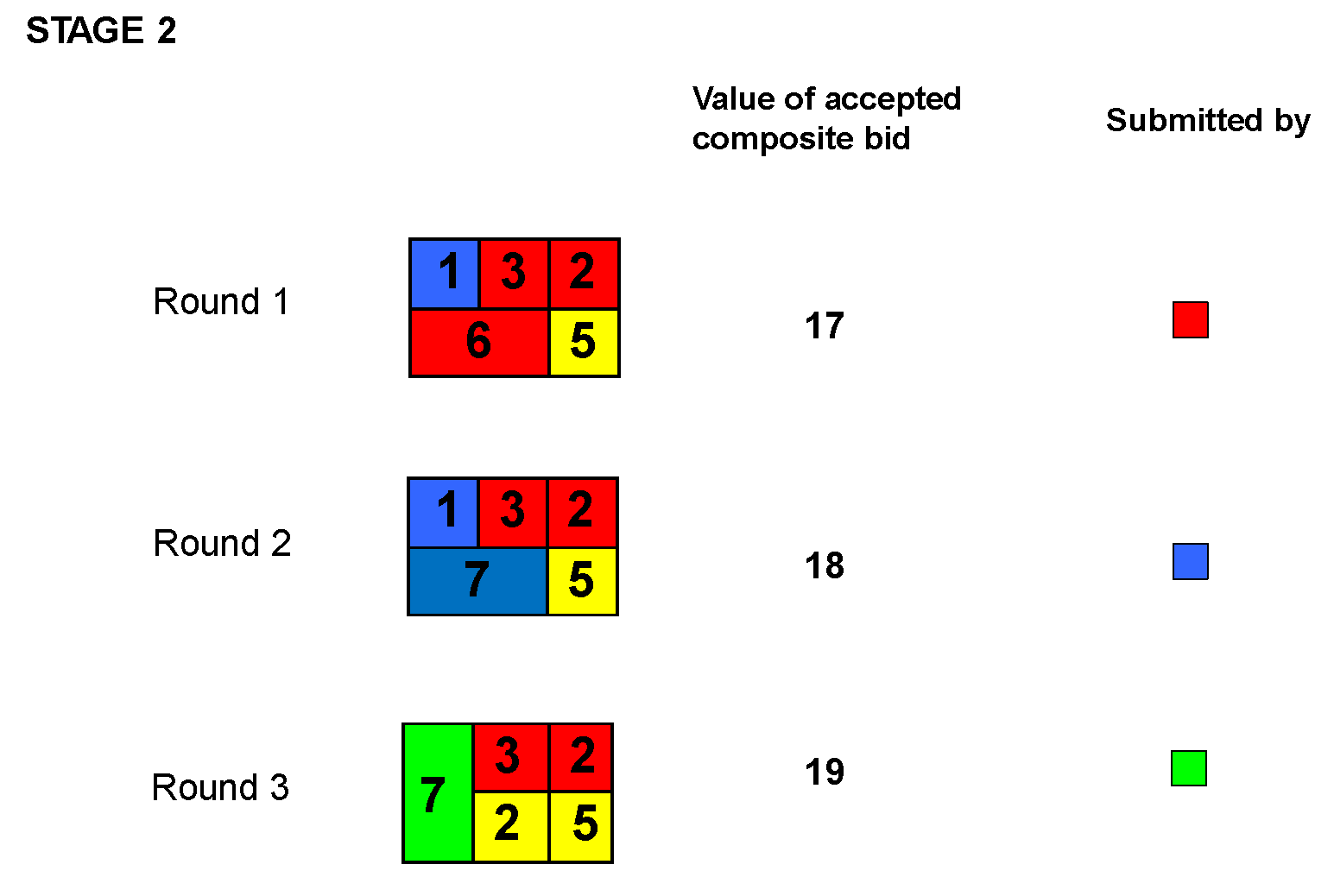
In round 2 of stage 2, blue has submitted the highest composite bid of 18, and in round 3 of stage 2, Green has submitted the highest composite bid of 19. Assuming that there is no more bidding in stage 2 after round 3, Green’s composite bid is accepted for stage 2, and the auction would continue to stages 3, 4, 5, and 6, where it concludes.
The Combinatorial Auctions book
The field of combinatorial auctions is comprised of many sub-topics based on three disciplines: economics, operations research—my discipline, which is essentially mathematical optimisation—and computer science. (Computer scientists have long studied how to process large amounts of data, a feature common to all combinatorial auctions.) Thus, no one person could write a book on combinatorial auctions. However, I could edit a book on combinatorial auctions, if I had as co-editors economist Peter Cramton and computer scientist Yoav Shoham, both at the top of their respective disciplines with respect to combinatorial auctions. Together, we three compiled a list of the key topics in the field and the ideal authors to write each chapter—all of whom agreed to participate. Nobel Laureate Vernon Smith wrote the book’s foreword; Nobel Laureate Roger Myerson wrote an endorsement of the book that appeared on the back cover. Many publishers were interested in the book, so we held an auction, awarding the book to the publisher offering to sell the book at the lowest price! The winner of Combinatorial Auctions was MIT Press.
One chapter, authored by Paul Milgrom with co-authors Peter Cramton and Lawrence Ausubel, proposed a procedure called the combinatorial clock auction, which requires the winner determination problem be solved not every round, but only once in the final round. That chapter was cited in Milgrom’s Nobel Prize—shared with Robert Wilson—awarded last October. The combinatorial clock auction has become the gold standard in combinatorial auctions, raising billions of pounds of revenue in auctions around the world. However, as combinatorial auctions continue to increase in size, the winner determination problem may soon become insurmountable. At that point, auctioneers might turn to using the PAUSE combinatorial auction procedure.
♣♣♣
Notes:
- The post expresses the views of its author(s), and do not necessarily represent those of LSE Business Review or the London School of Economics.
- Featured image by Daniel_B_photos, under a Pixabay licence
- When you leave a comment, you’re agreeing to our Comment Policy





