Modelling is vital if we are to control COVID-19, but it is not infallible. James Nguyen (University of London) and Roman Frigg (LSE) explain how epidemiological models work, and the importance of acknowledging the uncertainty inherent in their predictions.
James Nguyen and Roman Frigg are responding to Erica Thompson’s LSE Festival talk, How Can We Do Good Science with Models? Join in the discussion by posting a comment below.
“Models” form the basis of much of our scientific knowledge about the world. They are used to guide decisions that impact the lives of millions, if not billions, of people. Epidemiologists construct models of how a disease will spread through a population under different policy interventions, and climate scientists construct models of how the earth’s climate will change through time under different emission scenarios. The outputs of these models feed into governmental decision-making and form a significant part of what ministers refer to as “the science”, which they urge us to believe that they are following. But what are models, how do they work, and how confident should we be in their outputs?
From an abstract philosophical perspective, we can think about models as secondary systems that exist in their own right. Epidemiologists talk about how the “model-population” is separated into three compartments—“susceptible”, “infected”, and “recovered”—and explore how the relative size of these compartments change through time. In the more fine-grained “agent-based models”, such as the one developed at Imperial College London (ICL), they talk about how “agents” in the model move between households, workplaces, schools, and universities, and how different governmental policies might restrict the interactions they have with others. Climate scientists talk about how their models consist of grid cells and they conceptualise physical processes as the exchange of quantities between those grid cells. But all of these claims are, in the first instance, about the behaviour and dynamics of model-objects, rather than the actual world that we are ultimately interested in.
How, then, do—or should—scientists extract information about actual systems from their investigations on their models? The answer is that the models represent their targets. The notion of representation here is a familiar one to anyone who has used a map: by measuring the distance on the map between the points labelled “London” and “Edinburgh” and getting a number in centimetres, you can translate that distance, via the map’s scale (which is part of what we call a “key”), into a number in miles.
In the case of COVID-19 models, a crucial question arises. What are the “keys” associated with the epidemiological models that underpin our knowledge about how COVID-19 spreads across Britain? These cases are more complicated than the map example, since the representation is supposed to generate new information, rather than summarising things we already know. In the abstract, these keys associate facts about the model with claims about the world that we can be reasonably confident in. What these model-facts and target-claims are in each instance will depend on the concrete details of the model, and modelling context, in question.
Take the “SIR” model. As discussed above, this model involves a population with three compartments: “susceptible”, “infected”, and “recovered”. The model is specified by a system of differential equations that tell us how the size of these compartments change though time, based on parameters specifying the average number of sufficient-to-transmit contacts someone in the infected compartment has with someone in the susceptible compartment, and the average recovery time. If we specify these parameters, and if we set the initial sizes of the compartments based on our knowledge about early infections, then we can derive (or in some cases numerically estimate) a solution to the model in terms of the size of each compartment for each instant of time in the model. This gives us the model-facts required by the model’s key.
What about the key that we can use to deliver target-claims? The first thing to note is that the model is an abstraction: there are aspects of the target system that it makes no claims to represent. In the case of the SIR model, obvious examples include details of the pathogen: the model concerns rates of transmission, but remains silent about how transmission happens, and the effects of the disease on those who fall ill.
What about the things the model does represent? How should we associate model-facts with target-claims about rates of transmission in the actual world? A naïve way of interpreting the model would be to assume things like: if there are X infections in the model at time t, then there are X infections in the target at time t. Using such an “identity key”—a key that simply carries a model-fact over directly into an identical target-claim—has the benefit of being easy to understand, but it fails to appreciate the fact the models are, in general, not only abstractions, but also idealisations: they distort aspects of the target system that they represent. For example, the SIR model assumes homogenous mixing: contact between any two individuals is assumed equally likely—something that obviously isn’t the case in reality. Because of this, we shouldn’t expect what’s happening in the model to exactly match what’s happening in the target.
These issues do not go away with the development of more complex models. Consider ICL’s agent-based model. Whilst based on the SIR model (technically an SEIR model, since it includes an incubation period for the disease and so includes an “exposed” compartment), the ICL model provides a more fine-grained picture of the spread of COVID-19, which does not assume homogenous mixing. Agents of different ages “live” in the ICL model, and come into contact with one another. When an infected model individual comes into contact with a susceptible individual, there is a probability distribution associated with the disease being transmitted. Whether or not the susceptible person gets the disease depends on what the computer simulation draws from the probability distribution. As such, different runs of the model, even with the same initial conditions and parameter set-up (including for example, the government policy that is being modelled), can yield different scenario runs (which is not to say that the runs cannot be reproduced).
To account for the model’s “stochasticity”, scientists can perform multiple model runs and report the mean of values deemed significant (of, e.g. the number of cases requiring intensive care), or better, something like “in 95% of the model runs, there are between X and Y cases requiring intensive care (within a relevant time period)”. But there are still abstractions (e.g. there is still no mechanism for transmission) and idealisations in the model (e.g. at the time it assumed no contact tracing), and so we should still avoid naïvely inferring from this that there will be X and Y intensive care cases in the actual world (or that we should be 95% certain that this is the case).
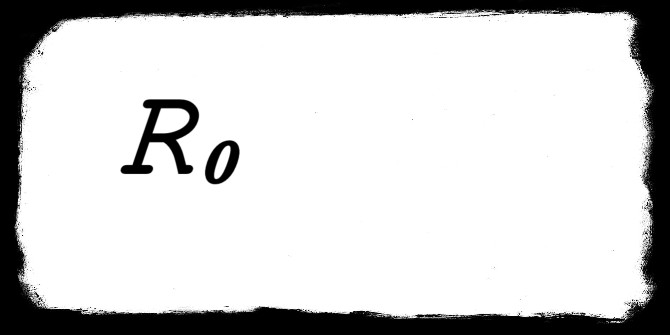
This is further complicated by the fact that the model needs to be “calibrated”, i.e. inputs are required in order for it to be run. This means specifying parameter values—like the infection fatality rate, hospitalisation or intensive care rate, and the now infamous R0 (the expected number of secondary infections per infected individual, assuming a completely susceptible population)—and initial conditions, like initial number of infections. At the beginning of the pandemic we were highly uncertain about at least some of these inputs. Due to the nature of these models, small differences in input values can produce large differences in outputs, and hence there is no guarantee that inputs that are close to each other also produce outputs that are close.
Modellers are aware of this, and perform so-called “sensitivity analyses” to see how their models behave with different inputs. For example, the ICL model was run with R0 values between 2 and 2.6, and they reported model outputs across these different parameterisations. But not all inputs were investigated in this way, and without exploring the space of inputs, we remain uncertain about how the model would behave when fed with the “true” inputs. So whilst 95% of the actual model runs performed might have had between X and Y cases requiring intensive care, we don’t know how much that relied on the precise details of the model inputs.
When making policy decisions in these sorts of contexts, we don’t expect the science to tell us definitively what will happen under each policy intervention being considered. But we might hope for some probabilistic information of the form: “under such and such an intervention, we are Z% confident that such and such will be the case”. So we want our model keys to match up model-facts with target-claims of this form. How should this work?
By now it should be clear that the fact that our models are idealised and based on data we are uncertain about, and others (things get even more complicated when we have multiple models to draw upon, something that happens in both climate science and epidemiology), we should be wary about using a key that takes “in 95% of the model runs, there are between X and Y cases requiring intensive care” to the claim that we should be 95% confident that in the actual world, there will be between X and Y such cases. We know that our models are distortions of their targets, and we are uncertain about the data we need to use to set up the data to get results in the first place. But at the same time, at least in certain instances, they are the best tools we have at our disposal. So what can we do?
We suggest that we should avoid the sheen of precision that accompanies investigations in model-land. At the very least we should consider how the sorts of uncertainties discussed above should impact our model outputs. We may consider lowering our certainty from 95% to something lower (as climate scientists did in the Fifth IPCC report); expanding the range from X and Y to something wider; or both (and then the question arises: what methods should scientists employ to do this?). As a result, what the model tells us about the target is, or should be, be less precise than it may originally appear. This makes decision-making on the basis of the model more difficult. But uncertainty and imprecision are facts of life when it comes to (much of) model-based science. As such, they should be communicated appropriately, to both policy-makers and the public more generally.
This post represents the views of the authors and not those of the COVID-19 blog, nor LSE.
How should we treat scientific models? Join the discussion below.





Hello. This is a great article, thank you. one of my biggest questions around CV19 modeling has been that it is impossible to know if the models are any good. If they turn out to be way below target (more pessimistic than what ends up happening), it’s because the interventions “worked”. Seems that this is related to falsifiability. In that sense, are these models even “scientific”?