 George Waters (BSc Economics) jointly won the British Society for the History of Mathematics Undergraduate Essay Prize in September 2021. His essay explored the use of mathematics to obtain consensus, and formed part of his assessment for our course on the History of Mathematics in Finance and Economics. George, pictured here with Professor Sarah Hart (President of the BSHM) at the award ceremony in October 2021, has kindly adapted his work into the piece below.
George Waters (BSc Economics) jointly won the British Society for the History of Mathematics Undergraduate Essay Prize in September 2021. His essay explored the use of mathematics to obtain consensus, and formed part of his assessment for our course on the History of Mathematics in Finance and Economics. George, pictured here with Professor Sarah Hart (President of the BSHM) at the award ceremony in October 2021, has kindly adapted his work into the piece below.
Combining the preferences of a group is a fundamental process for many aspects of our societies. The problem of generating a fair and justified first choice for a large group has been considered since well before the establishment of democratic societies. In Ancient Greece and Italy, voting for candidates was often done by clamouring and banging spears on shields, with the loudest uproar being interpreted as the most popular option. This is an example of possibly one of the original electoral processes humans have used. Our society has come a long way since then, but there are still a multitude of problems encountered when trying to reach consensus, even when very convoluted methods are employed. As shown in the first section, sources from as early as the medieval times show us how those studying voting systems recognised the problems in achieving a unanimous and fair decision. This piece will then further explore some of the various attempts to combine the preferences of individuals into a single ‘social’ preference, and the various problems encountered when doing so. There have been countless attempts at finding the best method of obtaining consensus, with this piece focussing on the most pertinent discoveries in the field, spanning centuries of developments.
Early Developments – Ramon Llull (c1232-1316)
One of the most common methods of trying to obtain a social preference is an election. In the 13th century, Ramon Llull (c1232-1316), a member of the Roman Catholic Church, was intrigued by traditional electoral methods used to elect Abbotts and Bishops in the church for many years. The traditional methods included Unanimity and Simple Majority, both of which came with various problems. Unanimity is when there are no objections to choosing a candidate, which makes decisions impossible if just one out of a group has an opposing opinion. Simple Majority voting is when a candidate needs over half of the votes to win, which would not be guaranteed to give a winner if there are more than two candidates. Llull was keen to find a better, more reliable way to elect Bishops and Abbots to the Christian church.
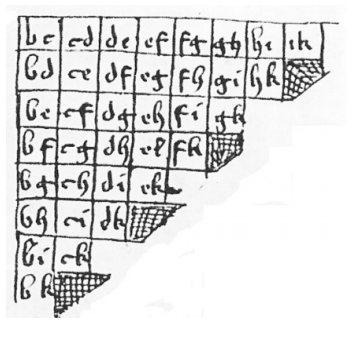
Llull’s idea was to execute the election in stages with only pairs, so that majority rule could always be used. The method is described using an example for nine candidates in De Arte Eleccionis [1]. In Figure 1, Llull gives an example with 9 candidates (b to k), with the curled ‘6’ like symbol representing the winner of the previous round. The winner then progresses downwards in the table, until all 9 candidates have been considered. Comparing nine candidates in pairs should require 36 comparisons, but Llull’s method only uses eight, with a ‘winner stays on’ system, similar to modern sport tournaments. This was the first ‘serious attempt’ at using simple majority in a real election with many candidates [2], and perhaps the first-time mathematics has been used to try to make the most efficient system. However, there is no evidence that Llull’s procedure was ever actually used in practice. Also, it requires that the preferences of a group be transitive, which is not always the case. The concept of transitivity will re-emerge later in the piece when discussing the 18th century mathematicians who studied it.
Llull did show impressive understanding of the nature of group decisions. For example, he identified the role of strategic voting and the problems this can cause [3]. Some theorists, such as the political scientist Josep Colomer, consider Llull to be the ‘founding father of voting theory and social choice theory’ [4]. Llull’s contributions were revolutionary, however the importance of many of the concepts and ideas he developed were not recognised and properly understood for hundreds of years.
Revival of Voting Theory in the 18th and 19th Century
In the 18th and 19th centuries, the idea of a ‘democratic government’ was growing in popularity, especially in Europe. Therefore, many mathematicians began applying themselves to voting theory. One of the main focuses of this academic pursuit was working on finding the best ‘social preference function’, which is an algorithm that considers the preferences of a group and gives out a consensus for the group as a whole. Through what some may consider to be unlikely motives, the following individuals have made germane discoveries in social choice theory, that were not always being pursued.
Jean-Charles de Borda (1733-1799)
Mathematical theory on elections was revived in France during the second half of the 18thcentury. The first thinker to develop a mathematical theory of elections was Jean-Charles de Borda (1733-1799). Borda’s interest in this field was not motivated by politics, but by his treasured membership to the French Academy of Sciences, for which he thought the electoral system could be improved [5].
He is most famous for a method which he studied, bearing his name, known as the Borda count. This method involves each of the voters ranking the candidates from most to least favoured. A number of points is then assigned to each candidate, corresponding to the number of candidates below them in the ranking. All the points are then added up for each candidate, and the candidate with the most points wins. Borda originally developed the method in 1770 for electing the members of the French Academy of Sciences; and published the work in 1781 as a paper in the Histoire de l’Académie Royale des Sciences, Paris [6]. The method was used at the Academy from 1784 until 1800, and it remains widely used today; in academic institutions as well as in electing corporate committees.
The Borda count is fraught with problems. One of its fundamental issues, the violation of the ‘Independence of Irrelevant Alternatives’, was discussed by Kenneth Arrow around 170 years after Borda first published his method. This issue is considered in more detail in the final section of this piece. In his work, Borda did not consider or give great intuition into the nature of group decisions. Nevertheless, according to Duncan Black, Borda’s work is a good first step in understanding the challenges of voting procedures that he highlights in his work. Black also recognised how Borda was able to suggest possible avenues of research into voting theory that could be developed further [7].
Marquis de Condorcet (1743-1794)
In both his mathematical and literary work, Marquis de Condorcet (1743-1794) was absorbed by elections. In 1785, being a member of the French Academy of Sciences (and a contemporary to Borda), he published his ‘Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix’ [8], in which he applied theories of probability to voting procedures. The Essai was divided into two sections, with the first being largely mathematical and the second indented to give an intuitive and philosophical account of his arguments. Similar to Borda, he also suggested new methods for elections. However, many found the Essai confusing and lacking in continuity between the mathematical and non-mathematical discussion. For example, Condorcet would dismiss his methods because of issues of impracticality, without discussing the theory behind them or the problems they solve.
Condorcet strongly disagreed with the Borda count; managing to highlight a problem which is now known as the Condorcet Paradox. When studying the preferences of individuals, economists often assume that transitivity will hold, which means that if option A is preferred to option B, and option B is preferred to C, then A will be preferred to C. This is assumed for individuals, which seems trivial; but what Condorcet demonstrated is that this does not always hold in a group when using ‘majority prefers’ (a simple majority system).

An interesting example of the Condorcet Paradox is Theresa May’s ‘Brexit conundrum’ in 2016. There were three options: to leave the European Union (EU) with the government’s deal; to remain; or to leave with no deal. Some polling data looked at what would happen if people were given a referendum between only two of the three options, and then what the outcome would be for each of the 3 pairs of options. The result was that leaving with a ‘deal’ was preferred to ‘remain’, ‘remain’ was preferred to ‘no deal’ but ‘no deal’ was preferred to ‘deal’ [9]. These preferences are cyclic, and highlight how with intransitive preferences, some systems might result in there being no majority winner. It is a striking example of how the problem highlighted by Condorcet centuries ago is still faced by politicians today.
Charles Dodgson (1832-1898)
Another mathematician to study the Condorcet Paradox was Charles Dodgson (1832-1898), better known by Lewis Carroll. Dodgson studied the possibility of letting people change their minds if the votes ended up being cyclic, or if there was a lack of majority. This concept might now be seen as similar to when parties form a coalition in governments.
Like Borda, Dodgson’s interest in voting originated from his position in an academic institution. As a member of the Governing Board of Christ Church College in Oxford, he wanted to find the fairest way to reach a decision on various matters. This interest then extended into politics, with Dodgson continuing to be driven by promoting a fair representation [10]. With electoral reform issues being discussed in the 1880s, Dodgson took an interest in the various issues of electoral systems, publishing multiple pamphlets on the topic in 1884, including Parliamentary Elections (1884) [11] and The Principles of Parliamentary Representation (1884) [12]. He applied his mathematical aptitude to this problem, with many of the ideas in his reasoning being what is now known as game theory. His contributions to voting theory and game theory were significant, with him being an early pioneer of the latter [13].
Kenneth Arrow (1921-2017)
Kenneth Arrow (1921-2017) was an American economist who made significant contributions to various branches of economics throughout the 20th and 21st century. After completing his bachelor’s degrees [14], he used his aptitude for high level mathematics to assist in making pertinent discoveries in social choice theory. Few economists before him had applied advanced mathematics to specialist fields in economics. One of Arrow’s most influential contributions to social choice theory is an impressive result known as Arrow’s Impossibility Theorem. It begins with four reasonable axioms that a social preference function should ideally satisfy. These are as follows:
- Non-Dictator – The ranking is not simply one person’s ranking.
- Unanimity – If everyone prefers one policy to another, then so should the ranking.
- Universality – The voting system should always return one clear result.
- Independence of Irrelevant Alternatives (IIA) – The ranking of one option above another should only depend on how individual votes ranked those two options, and not how they ranked them when compared to a third alternative. [15]
IIA is more complicated than the first three. It rules out the Borda count and other similar procedures. This is because in the Borda count, one of the voters can change their ranking between two individuals who are not in the lead and in turn alter the ranking between the winning two [16]. IIA highlights a fundamental issue with the use of the Borda count.
Arrow proved mathematically when there are more than two voters, no procedure exists for achieving a consensus that will satisfy all four of these axioms. Therefore, all voting procedures are somewhat imperfect. Arrow worked on this for his PhD thesis, eventually publishing his full ‘impossibility theorem’ with the mathematical proof in his 1951 book Social Choice and Individual Values [17].
People studying social choice (such as those mentioned previously) had always been aware of what seemed to be insurmountable difficulties faced when attempting to conjure the best social preference function. What Arrow managed to do was prove that it is in fact impossible to find one that is ‘perfect’, which he did with sweeping generality. This result is fundamental to social choice theory, with it still being studied today in both economics and politics.
Conclusion
What is perhaps most fascinating about the issues surrounding social choice is how relevant they remain, yet there are still many problems without a perfect solution. The idea of the ‘best’ voting procedure is somewhat subjective, with each method regarding certain properties as more important than others. To see evidence of this, one must simply look at how varied elections are in different countries, regions and organisations around the world. Each method must adapt to the specific features that are deemed to be the most important, depending on a host of factors including geographic and demographic characteristics.
A lot of work continues today regarding the challenge of finding the best social preference function. However, this involves finding the one with the least problems, or at least with what the least important issues are in the context. The conception of Arrow’s theorem has shifted the direction of the field of social choice to a discussion on what the most important features of a social preference function are. Questions surrounding whether all elections are fair and just are still extremely relevant. An example of this would be the 2016 US elections, with Hillary Clinton winning the Popular vote but losing the ‘Electoral College’ result that the presidency depends upon.
The respective successes of the numerous figures mentioned in this particular field can be somewhat attributed to their applications of mathematics to their interest in social choice. For example, probability (particularly by Condorcet), game theory by Dodgson and aspects of analysis in Arrow’s proof of his Impossibility theorem. Expressing social preferences mathematically allowed all the figures discussed in this piece to further the theory of social choice, which has been fundamental to the conception and progress of successful democracies.
References
[1] Llull, R., 1299. De Arte Eleccionis. from Cod.Cus.83, f.47v-48r. Available at http://www.uni-augsburg.de/llull/ [Accessed 1st July. 2021]
[2] Colomer, J. (2013). Ramon Llull: From ‘Ars Electionis’ to Social Choice Theory. Social Choice and Welfare, 40(2) p. 320.
[3] Tangian, A. (2020). Analytical theory of democracy. Switzerland: Springer International Publishing, p. 98.
[4] Colomer, J. (2013). Ramon Llull: From ‘Ars Electionis’ to Social Choice Theory. Social Choice and Welfare, 40(2) p. 320.
[5] Black, D. (1958). The Theory of Committees and Elections 2nd Edition. Cambridge: University Press.
[6] Borda, J.-C. (1781). Mémoire sur les élections au scrutin. Paris: Histoire de l’Académie Royale des Sciences.
[7] Black, D. (1958). The Theory of Committees and Elections 2nd Edition. Cambridge: University Press.
[8] Condorcet, M. d. (1785). Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix. Paris: de l’Impr. royale.
[9] Kaye, S. (2018). Deal > Remain > No-deal > Deal: Brexit and the Condorcet paradox. LSE BPP, [Online]. Available at: https://blogs.lse.ac.uk/politicsandpolicy/brexit-condorcet/ [Accessed 1st July. 2021]
[10] Abeles, F. F. (2001). (Abeles’ Annotations of ) The Political Pamphlets and Letters of Charles Lutwidge Dodgson and Related Pieces: A Mathematical Approach. Charlottesville: University Press of Virginia
[11] Dodgson, C. (1884). Parliamentary Elections.
[12] Dodgson, C. (1884). The Principles of Parliamentary Representation.
[13] Abeles, F. F. (2001). (Abeles’ Annotations of ) The Political Pamphlets and Letters of Charles Lutwidge Dodgson and Related Pieces: A Mathematical Approach. Charlottesville: University Press of Virginia
[14] Weinstein, M. M. (2017). Kenneth Arrow, Nobel-Winning Economist Whose Influence Spanned Decades, Dies at 95. New York Times [Online] Available at: https://www.nytimes.com/2017/02/21/business/economy/kenneth-arrow-dead-nobel-laureate-in-economics.html [Accessed on 1st July. 2021]
[15] Arrow, K. J. (1951). Social Choice and Individual Values. New York: John Wiley & Sons.
[16] Arrow, K. J. (1951). Social Choice and Individual Values. New York: John Wiley & Sons.
[17] Arrow, K. J. (1951). Social Choice and Individual Values. New York: John Wiley & Sons.






Interesting and informative read! Fascinating writing on the ‘Brexit conundrum’. Great stuff George