Mass media routinely portray information about COVID-19 deaths on logarithmic graphs. But do their readers understand them? Alessandro Romano, Chiara Sotis, Goran Dominioni, and Sebastián Guidi carried out an experiment which suggests that they don’t. What is perhaps more relevant: respondents looking at a linear scale graph have different attitudes and policy preferences towards the pandemic than those shown the same data on a logarithmic graph. Consequently, merely changing the scale on which the data is presented can alter public policy preferences and the level of worry, even at a time when people are routinely exposed to a lot of COVID-19 related information. Based on these findings, they call for the use of linear scale graphs by media and government agencies.
The fact that the framing of information can dramatically alter how we react to it will hardly surprise any reader of this blog. Incidentally, the canonical example of framing effects involves an epidemic: a disease that kills 200 out of 600 people is considered worse than one in which 400 people survive. Whereas this imaginary epidemic was just a thought experiment, an actual global pandemic turns out to be an unfortunate laboratory for framing effects. In a recent experiment, we show how framing crucially affects people’s responses to one of the most important building blocks of the COVID-19 informational puzzle: the number of deaths. We show that the logarithmic scale graphs that the media routinely use to display this information are poorly understood by the public and affect people’s attitudes and policy preferences towards the pandemic. This finding has important implications because during a pandemic, even more than usually, the public depends on the media to convey understandable information in order to make informed decisions regarding health-protective behaviours.
Many media outlets portray information about the number of COVID-19 cases and deaths using a logarithmic scale graph. At first sight, this seems sensible. In fact, many of them defend their decision by showing how much better these charts are in conveying information about the exponential nature of the contagion. For history lovers, the popular economist Irving Fisher also believed this, which led him to strongly advocate for their use in 1917 (right before the Spanish Flu rendered them tragically relevant). Fisher was ecstatic about this scale: “When one is once accustomed to it, it never misleads.” It turns out, however, that even specialized scientists don’t get used to it. Not surprisingly, neither does the general public.
We conducted a between-subjects experiment to test whether people had a better understanding of graphs in a logarithmic or in a linear scale, and whether the scale in which the chart is shown affects their level of worry and their policy preferences. Half of our n=2000 sample of US residents was shown the progression of COVID-19 related deaths in the US at the time of the survey plotted on a logarithmic scale. The other half received exactly the same information–this time plotted on a good old linear scale.
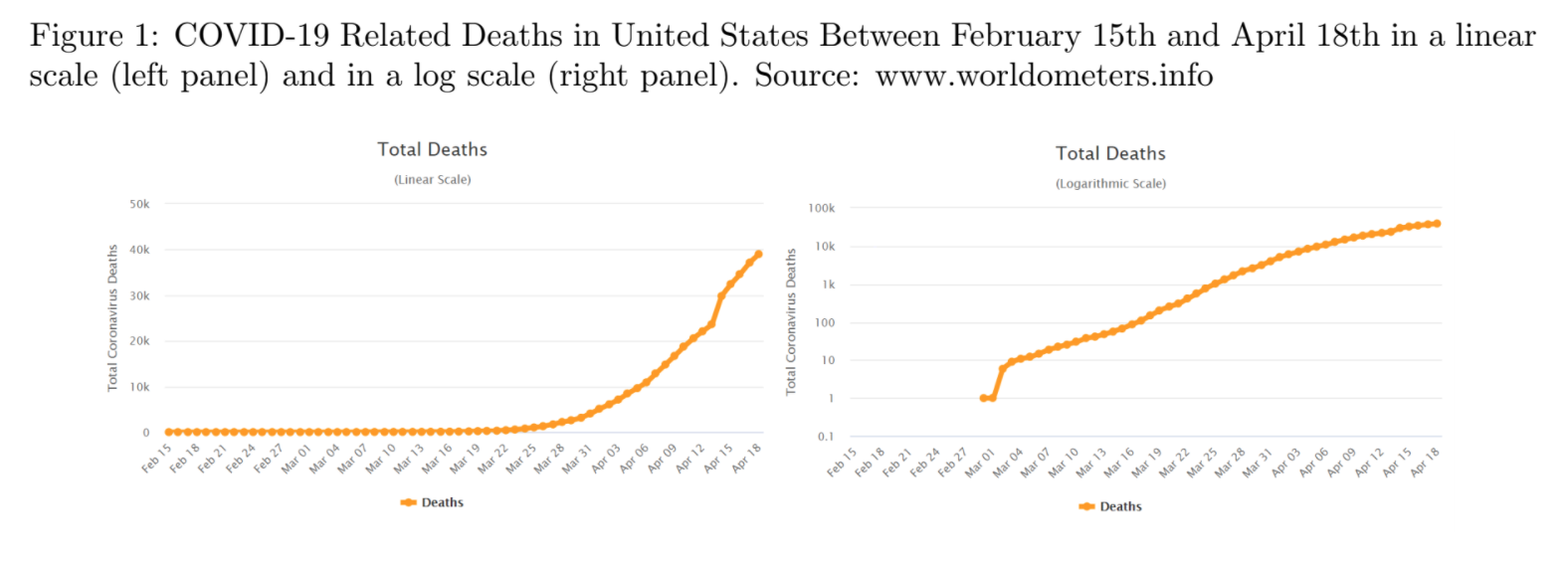
Contrary to Fisher’s optimism, we find that the group who read the information on a logarithmic scale has a much lower level of comprehension of the graph: only 40.66% of them could respond correctly to a basic question about the graph (whether there were more deaths in one week or another), contrasted to 83.79% of respondents on the linear scale. Moreover, people in the logarithmic group also proved to be worse at making predictions on the evolution of the pandemic: they predicted, on average, 71,250 deaths for a week after the experiment was taken, whereas the linear group predicted 63,429 (our ARIMA forecasting model indicated 55,791, and the actual number of deaths on that date was 54,256). Nevertheless, respondents in both groups stated a similar level of confidence in their answers.
Furthermore, we tested whether the scale used affects the respondents’ attitudes towards the pandemic. It looks like it does. First, we find that despite predicting a higher number of deaths, people who were shown the logarithmic scale chart declare to be less worried about the health crisis caused by the coronavirus.
Divergences, however, don’t stop there. The scale of the graph they see affects people’s responses concerning their policy preferences and stated behaviours. Ceteris paribus, respondents who see the information on the linear scale graphs support less strongly the policy of keeping non-essential businesses closed than those who look at the logarithmic one — although they also favour reopening them later. At the same time, those who see the linear graph are more willing to support a hypothetical state-level tax aimed at providing citizens with masks.
A possible explanation of our finding is that the linear scale gives the impression of a growing pandemic, without any sign of improvement. At the same time, the curve on the logarithmic scale looks flatter and reassuring. However, it has a higher end-point value on the Y-axis, which might act as an anchor when assessing the short-term evolution of the pandemic. Therefore, while the logarithmic group predicts more deaths in the short term due to the higher anchor, the linear group expects the crisis to last longer. Consequently, the linear group is more worried about the health crisis, while anticipates to wear masks less often in order to ration them.
Admittedly, we cannot know which policy preferences are superior. However, we do know that unlike the people who saw the graph on a logarithmic scale, the people exposed to a linear scale graph can form their preferences based on information that they can understand better. This is a strong enough reason to suggest that mass media and policymakers should always describe the evolution of the pandemic using a graph on a linear scale, or at least they should show both scales. After all, if we want people to wash their hands and keep six feet from each other, they better understand what’s going on.
This post represents the views of the authors and not those of the COVID-19 blog or LSE. A pre-print of the experiment can be found here, and the corresponding author can be reached out at alessandro.romano@yale.edu.




The public don’t understand Relative Risks either. Or any statistical manipulation.
Our education system seems to systematically dumb down the public – particularly in mathematical and historical subjects. If I were attracted to conspiracy theories, I might think that a public which can’t count, and which forgets any lessons learned more than 20 years ago, made bureaucratic hegemony particularly easy for the technocrats…
Thanks for your comment! We like to see the glass half full. When presented with the linear scale, people showed a good understanding of the graphs and made accurate predictions. We just think the log scale can be confusing, as shown also by previous research (Menge et al. 2018, linked in the article).
I would push back on this and say that, it’s not that our education system dumbs down the public, but rather it inadequately educates students on nonlinear thinking. Humans by nature are linear, cause and effect thinkers and it’s a bit foreign to step outside of that unless taught how to, and even more importantly, how important nonlinear thinking is in the real world.
Some people cannot differentiate speed from acceleration. It’s not like they flunked out of Calculus 101. It’s like they never took it in the first goddamn place. Like Trump voters. Better to dumb it down with pure linear functionality.
While I bristle re “dumbing it down” I wouldn’t jump from any study to communication recommendations or policy nudging so quickly. Here in the US we’ve been grappling with what’s involved with bringing all folks along when it comes to public health and science.
More than 40 years of large-scale study of public understanding of science shows us that less than 1/3 of the US population is science literate. Are clear about when antibiotics are effective, can name the steps in the scientific method, or understand why a control group is necessary in a new drug’s development. For almost 30 years similar surveys show us that more than half of the adults in the US are low health literate – can adequately find, understand and use health information well. General functional literacy is also poor – and that includes NUMERACY – ability to work with numbers and their visual representations.
So as experts and the media converse about COVID we need to confront the fact that much of this is simply out of reach of millions – novel virus, chain of transmission, modeling, rate of infection, flattening the curve, social distancing, high throughput vaccine development, antibody testing and immunity passports.
There is no one best remedy. We are clearly not all in this together ( strange I’m working on a piece with that name) Have enjoyed your blog.
Fascinating post, thank you!
Can you clarify this statement though: “respondents who see the information on the linear scale graphs support less strongly the policy of keeping non-essential businesses closed than those who look at the logarithmic one”, which would seem to contradict the following: “A possible explanation of our finding is that the linear scale gives the impression of a growing pandemic, without any sign of improvement.”
Would the latter not imply that those reading the linear graph ought to support *more* strongly the policy of keeping non-essential businesses closed? Or am I missing something obvious?
Hi Bob,
Thank you very much for your kind words! You raise a very good point. For the sake of transparency, we pre-registered all the hypotheses we made. While the general direction of the findings is consistent with what we had in mind, some results were unexpected. This is one of those, which is why we flag it also in the blog post. The explanation we have for this finding is that the linear scale gives the impression of something that will last for a very long time, as it doesn’t look like the curve is “flattening”. Therefore, as it is impossible to freeze the economy for many months, people might think it is better to just reopen earlier. To put it differently, if you tell somebody that the virus can be contained by shutting down the economy for two months, they are likely to support the shut down. However, if you tell them that we need to shut down the economy for 2 years before we see improvements, they might prefer to keep economy open and go for other containment strategies. Admittedly, this is just our reading of the results and not something we can test given our data.
Best,
Chiara
Hi Richard! Thanks for your comment.
It’s not clear to us whether humans are “linear” by nature (there is no shortage of evidence showing that children and non-Western adults intuitively plot numbers on a logarithmic, rather than linear, scale: https://science.sciencemag.org/content/sci/320/5880/1217.full.pdf among many others).
It would indeed be very interesting to test further how people understand logarithmic growth, and to what extent “linear” education interferes with it. But as for our results go, be it nature or education, it looks that linear scale graphs help to better understand the spread of COVID-19.
I guess it largely depends on what you want to portray. If you want to scare the public use linear, if you want to reassure use logarithmic.
If you want to allow your readers to understand the magnitude of the problem you need to scale by the population. Is 40K deaths a lot or a little in comparison to the normal number of deaths?
Thank you for your comment! We agree with you completely. This is exactly the issue we wanted to raise. There is no “neutral” way to frame the data. The effect of presenting total numbers vs numbers scaled by the population would be a very interesting experiment and pretty easy to carry out!
We agree with you completely. This is exactly the issue we wanted to raise. There is no “neutral” way to plot data on a graph. Testing the effect of presenting total numbers vs numbers scaled by the population would be a very interesting as well. It would also be pretty easy to do!
Thanks for the analysis. It’s much needed. As a former infographics editor at a major newspaper, I always thought one of my strengths was a lack of math skills. If I could understand a chart, perhaps readers could, too. And yeah, I never used a log chart. Likewise always include the zero line or indicate it’s absence. Two cardinal rules of chart-making for the general public.
Thank you for your interest in our work!. We really appreciate your words, as we do not have any
experience working with newspapers, so it is great to know that the points we made resonate with
somebody who worked at a major newspaper!
I am concerned that the findings of better comprehension with linear graphs may say more about the choice of questions used to test comprehension than about the innate superiority of linear plots.
As far as I can see, all three “comprehension” questions are testing much the same thing: the participants’ ability to eyeball the rate of change in a one-week period. One would expect better results from linear graphs here – it’s very easy to compare two slopes, or to extrapolate a slope for a short distance. (I’d also note that in the range of interest, the linear plot is marked in intervals of 10k, whereas the log graph has nothing between 10k and 100k.)
But there are other questions that may be just as important. For instance – have changes in behaviour after a given time point slowed the rate of transmission? What numbers might we expect *four* weeks into the future, a time scale over which the nonlinear nature of the curve becomes far more important than for a one-week forecast?
For both these questions, I suspect that subjects viewing a logarithmic chart might do better (especially with some more markings on the y-axis). But the questions don’t cover this territory.
Hi Geoffrey. Thank you for the very interesting comment! This is great food for thought. We can’t rule out that people that are shown log would do better with a different set of questions, or a different log scale graph. We tried to ask questions that we felt were relevant. For instance, how a person behaves tomorrow might be more influenced by her short term-forecasting (one week) than her mid-term forecasting (four weeks). Moreover, we picked a graph from a widely used website (https://www.worldometers.info/) to increase external validity. But we’d be very curious to see studies asking different questions. For example, what happens when more than one curve is plotted on the graph? Some newspapers, like the Financial Times, do it.
We also agree that there are many details of a graph that can affect how people react to it. Your example of the values on the Y-axis is a case in point. However, one could imagine that people are more easily influenced by graphs features if they do not properly understand the content of the graph. Consequently, one possible claim is that graphs that are easy to understand should be used, exactly because we cannot predict the impact on people’s mind of all the details of a graph.
Nice insights about adult numeracy & Covid. I’ve also been blogging about this and public understanding of Covid issues. You can view 3 online seminars I gave in April at.
https://publiclinguist.blogspot.com/2020/04/lost-in-covid-numbers-weve-picked-most.html?m=1
Thank you very much Christina! We will certainly look into them!
Yeah, the innumeracy of the general public is an ongoing problem.
One of the things I’ve found is that the introductory framing of graphs, charts, contributes to how the reader approaches the visual array and what they expect to find. This ultimately influences the readability / usability of the text. For instance, using a contemporary situation, NYC residents can check out the daily morbidity and mortality numbers (COVID) online and they see the following introductory statement before they view a bar graph:
“This chart shows the number of confirmed cases by diagnosis date, hospitalizations by admission, date and deaths by date of death from COVID 19 on a daily basis since February 29.”
In linguistics we refer to these introductions as sorts of “superordinate pre-statements” that signal to the reader, “get ready to read about……” But in this case the pre-statement is way to packed. We’ve found more limited, directed pre-statements influence comprehension.
Have you looked at this type of framing in your work. How were the charts presented?
Thanks again,
Christina
Thanks again Cristina! We did have what you call a pre-statement to explain the respondents what they would be looking at and to explain the scales used. We then reduced the explanation for later questions, but a short statement was accompanying the graphs in every question. To increase external validity, the explanations mirrored very closely the ones presented by the New York Times in its articles. However, we’re really not experts in linguistics. We agree with you that it would be very interesting to study how different framings affect understanding and policy preferences. We should talk about it!
Here’s some questions I ask when creating the headline and intro/preamble to a graphic:
— Can the headline suffice without further intro text?
— Don’t restate anything in the intro that’s clear and obvious in the graphic.
— Use phraseology rather than complete sentences to keep the text brief if possible.
— Don’t use extra words like “This graphic shows.” We know it’s a graphic. We know it’s supposed to show something.
— If the intro goes beyond a brief phrase or two, step back and ask why the graphic needs explaining. The best graphics will need very little if any setup. Lots of setup can indicate there may be serious flaws in the graphic.
— Consider the context/setting. If the graphic will stand alone, be shared, the need for an intro may be greater than if it’s embedded in a story and not intended to be consumed in a vaccum.
I fail at this a lot. I get wordy. That’s where it’s crucial to show a graphic to someone who is not familiar with the work, to get a raw reaction. If they don’t grasp it’s intent and meaning quickly, I know I have a problem. People should not have to decipher an infographic, no more than we’d expect them to decipher an article.
See Napoleon’s March, held up by Tufte as one of the best infographics ever. A casual observer with little knowledge of history can glean the graphics methods, scope and rough conclusions even without understanding the language it was created in. Yes, there’s a long intro, but it’s additive, not critical. https://www.edwardtufte.com/tufte/posters
This is all great, thank you! (And the Napoleon graph is gorgeous)
As Chiara says above, we tried to mimic our introductions as best as we could with those actually used in newspapers (while also minding symmetry).
That said, there are tons of things that would be interesting to test in these graphs and introductions that we couldn’t possibly do, but if you have any idea we could discuss it!
Did you test comprehension after showing *both* graphs, side by side? Might that improve comprehension each presented separately?
Also, what effect difference would you expect to see if the charts showed comparable data (e.g. country-by-country death rates, as discussed in the Vox article you linked)? Would you expect a smaller effect?
IMO these are both important hypotheses to explore before concluding that “the public does not understand logarithmic graphs.”
Excellent point. It seems that more points of analysis are required to reach this conclusion.
In the United Kingdom, some national newspapers have used (the practice has stopped) a single log graph to compare COVID-19 infection rates in two (or several) countries. Given (1) the compression at the higher end of the scale, and (2) the supplementary ‘infographic’ function of the illustration (précis, rather than technical discourse; a snapshot of where things stand in different parts of the world ), it may be more accurate to conclude that newspaper editors do not always deploy log graphs appropriately.
Hi Kristin,
Those are great questions. We considered adding a treatment with both scales, but we opted for larger sample size in the end to increase our statistical power. Our original hypothesis was that people seeing both graphs would have just relied on the linear scale, or at least that we would have no way to test this. Of course, we do not know if this hypothesis is correct and we hope future studies will investigate it.
Testing what happens when a single chart shows comparable data would also be very interesting. One of our questions about understanding in fact shows two curves (male and female infected on a hypothetical disease we borrowed from a previous study on graph comprehension), and it also shows that readers overwhelmingly understand better the linear rather than log scales. We cannot rule out that some particular questions (ie, “when will the number of infected in country A catch up with the number of infected in country B”) would have a better record on a log scale–it would be great to test it. But, however, let’s say that’s the case: In what sense could we say they *understood* the graph, when we have evidence that they don’t understand well its building blocks (ie, individual curves)?
In any case, we ultimately decided for a single curve for an external validity reason: most newspapers we surveyed show one country curves, many on log scales.
In other words, I think for now we can conclude that (there is some evidence that) “the public does not understand well logarithmic graphs,” which doesn’t have to mean they don’t understand them in any context or no matter how much additional cues they receive. In fact, as you say, future research could show that “the public does not understand logarithmic graphs, unless shown together with a linear scale graph/unless they show a comparison across multiple curves.”
I’m sorry not to have the time to read ALL of the comments, so I might be repetitive.
However, I just find it impossible to believe that “specialized scientists” cannot fully understand a semi-log graph, or that anyone finds it easier to extrapolate the ordinate value for higher ranges of the abscissa, after an exponential growth curve has turned nearly vertical.
I am a “specialized” physicist and engineer.
Lastly, nothing would surprise me about the mathematical inadequacies of the average American: just look the OECD PISA test results or look up Jay Leno’s Jay-Walking interviews on YouTube.
There’s a ton of research on graph competencies in various communities done by Wolff-Michael Roth, and some by me (G. Michael Bowen…mine mostly focuses on BSc graduates). Nice study you’ve done here, altho’ the results aren’t all that surprising….but nicely specific with Covid, so kudos to you all.
Hi Michael, thank you!
Your research looks terrific. We are not from the field, so we’d be happy to discuss about it and learn from you if you have time.
Superb piece of work. Some of your findings initially appeared counter-intuitive to me but your reasoning is ultimately convincing. This really does highlight the importance of data presentation to non-specialists, particularly where people’s decisions may be driven by a poor understanding of what the data represent.
Well done.
Hi James, thank you for your kind words! You are right, some results are counter intuitive. In fact, we confess that some of our findings are not in line with our pre-registered hypotheses. However, we are aware of other researchers that are observing similar results. That is, people who think that the pandemic will last longer might be less likely to take strong precautions.
Clearly shown is the need for better math education.
Marking axes clearly and a brief, simple explanation are also very important.
Many times, what is trivial for the authors is not at all trivial for the readers.
Hi Lou, thank you for your comment! We agree. Whether something is trivial is very likely to depend on the audience. We did offer a short explanation of the scale to the readers but have no way of directly testing how that affected their understanding.
I think your questions are not testing the appropriate measure of graph comprehension, and also are not the right questions for gauging the appropriateness of the policy response.
Readers’ inability to forecast deaths a week hence (or infer deaths over the past week) surely just reflects the difficulty of interpolating between the grid points on a log scale. In any case this is not what log graphs are designed to show; they are for gauging whether the growth rate has changed. You should ask subjects how they think the growth rate of infections has changed. I imagine those that see the log chart would do better.
Moreover, surely a better test of whether readers are making the right inferences to gauge the appropriate policy response is whether they can forecast total deaths (barring a second wave). I suspect those shown the log graph would do much better here as well, and hence their more sanguine approach to the virus might be entirely appropriate. Obviously we don’t have the data to test their predictions yet, but I hope you asked the subjects this as well in anticipation.
Hi Lee, thank you very much for your useful comment!
We believe that the number of deaths at the end of the pandemic depends on too many factors that cannot be derived from the graph. For instance, it depends on how and when Trump and the Governors of the various States decide to reopen the economy. A bad guess in this sense doesn’t necessarily reflect a poor understanding of the graph.
It can be that respondents in the log group could have performed better had we asked different questions. We agree that it would be interesting to see studies that do just that, and test comprehension by asking different questions.
The virus exponential growth is no different to a financial index, therefore logarithmic axis is preferable. Linear is passable while growth is slow, but if it speeds up, the data near the origin of the chart becomes hard to visualise.
Hi David, thank you for your comment! We believe that the target audience is the key factor to consider when deciding how to represent data. For this reason, what could work for financial professionals might not work for the general public.
In my experience, people intuitively understand linear relationships, but unless they constantly work with nonlinear data, have difficulty with non-linear relationships and the graphic display thereof. For example, side by side columns of equal width are understood easily, but circles of different sizes, which vary in size with the square of the radius, are less well understood. The findings of your study are not surprising, and underscore the wisdom of avoiding log y scales whenever possible.
Thank you for discussing this issue! Not only are log graphs commonly used for the general public, but they aren’t even explained. I agree with the newspaper graphics designer’s comment above about including the base line as well. I have noticed something regarding graphs in the US Covid-19 news, which is their absence, even on reputable networks! There is unending talk about “flattening the curve” but the curve itself – the graph – is rarely shown. Visual display of data is so much easier to absorb than a list of numbers or verbal description. Do you have any idea why graphs are not used much in US news?
Very interesting analysis. Thanks for doing this. Are you concluding the media are culpable in misleading readers by portraying information logarithmically? It might be worth noting that policy makers must use logarithmically presented data to inform policy decisions. There is no information contained in the linear data to inform correct policy. So in that sense, media using logarithmic data is not wrong. Both linear data and the metric “totals” have compounding weaknesses in that they don’t convey information useful for policy making. They are like looking at a boxscore of a ball game the day after. You can see what happened, but you can’t use a boxscore to predict what will happen in the next game.
It must be a challenge for the media to present the best information since the reference sites (including the ones you used) all present “totals” data. It takes a little work and know-how to extract the useful metrics “velocity” (or rate of growth) and “deceleration” from these data. It’s easy enough if you know how, and in fact you can eyeball it by looking at the slope of the logarithmic curve and the change in slope of the logarithmic curve. But it can also be extracted and presented in simple bar graphs that anyone can understand. When you think about “R”, velocity is the best facsimile for R. And, if the goal of policy decisions is to reduce R below 1, then deceleration is a metric that discloses the effectiveness of policy decisions. I posit it would be most helpful if media started reporting on growth rates and deceleration instead of totals.
Problem with this is (as a layperson) I’ve not seen log-scale graphs being used, especially not for incident counts. Likely different for experts in the field, but all the graphs I’ve seen are linear. Colorado for example: https://covid19.colorado.gov/hospital-data
So this seems to be criticizing a practice (log-scale graphs for incident counts, to public audience) that doesn’t exist.
The real title should be: logarithmic scale is deceitful, something that should be used very carefully in very special cases, not everywhere. one good example: growth of top500 supercomputers power.
It’s very easy to lie with the logarithmic scale and it’s often used for this purpose.
I use log-scale graphs all the time in my engineering profession but I too would have a hard time interpolating on that log-scale with any kind of accuracy. However, neither graph is really great at answering the questions you are asking. You need to plot daily numbers with a moving average (not a cumulative total) to easily visualize whether it is growing or not. These cumulative total graphs need to stop being shown by everyone. They are misleading.
Hi Logan,
Thanks for the interesting comment! It would be very interesting to compare the reactions to the graphs used in our experiment (and by the media!) with the reactions to the graph you suggest. It could very well be that the graph you propose would be much better to convey information.
I like ‘Playing’ with data and when I saw a site that listed daily numbers, by state, of covid deaths and cases, I jumped in. I wish they had the number of tests given, but I’ll take what I can get. So I charted out the cumulative numbers and someone pointed out that it would never show a decrease. So I took the total numbers from the last 14 days and added them together each in their own category. But trying to graph them out, the cases were way high compared to the deaths. So I couldn’t show any comparison between the two numbers. So, maybe incorrectly, I took the square root of the number of cases, wich brought them to a level where I could see if cases went up, the deaths appeared to follow. I just wanterd to see the two in comparison. My brothers suggested logs, but I never knew what they were and how they actually worked. After reading som on them, I’m still lost with them. Question being, is the square root a viable way to breing these numbers down to a reasonable size , be an accurate ‘view’ of the two sets of numbers?
Thanks,
From someone who just plays with data for fun.
Instead of taking a square root, I’d suggest rescaling to make the two series similar in size. If you’re using something like Excel, you can do this by creating a secondary y-axis (see https://support.microsoft.com/en-us/topic/add-or-remove-a-secondary-axis-in-a-chart-in-excel-91da1e2f-5db1-41e9-8908-e1a2e14dd5a9 for tips) or you can plot deaths vs. thousands of cases.
A logarithmic scaled chart can be a bit confusing, when it isn’t even visibly labeled as such it’s an absolute guarantee that it’s going to be misread.
So the article says that a lot of the charts the media has been showing are log charts, and frankly, that’s news to me!
Thank you for this analysis. It is really interesting to see how difficult it is for the public to interpret the results on the plot.
However I would assume that there is an even bigger issue in interpretation of the plot when it comes to the pandemic – and that is what is chosen to be plotted at all, namely the total number of deaths. By definition, it can ever only increase – which is a serious weakness. Any viewer of the graph has to ascertain worsening of the disease by looking at changes over time rather than the absolute values. I would assume that instead plotting “number of deaths per week” would make it much easier for people to understand what is actually happening. Also the question asking after the total number of deaths the week after the plot was made feels odd. Why would you ask for the total, rather than number of additional deaths in the next week? The question seems to be guided by how the graph portrays information, rather than what is of actual interest related to the pandemic and the type of information asked for.
Overall it is relatively well known that humans have an easier time gaining information when they can look at absolutes rather than changes. And changes should be linear to make it easier. Which is an easy explanation of why the logarithmic graph fails here – the behavior of the curve is simply not exponential.
Hi Holger,
Thanks for the comment! Just to be clear, we were not implying that the graphs we used are the best. We were merely replicating what is often done in widely used media. We agree with you that other ways of conveying information, like the one you suggest, could prove to be superior. Indeed, it would be very interesting to test the assumption that you make.
You might have saved yourselves considerable research effort by skipping epidemiology altogether and checking the difficulty modelers have in explaining to the public WHY an earthquake 9 on the Richter scale is So Much Worse than one measured at 8.9. I had this problem with the 2011 Tohoku earthquake, originally announced as 8.9, revised to 9, where many scientists ignored the difference, focusing instead on the reactor meltdown (which killed nobody) while the earthquake/tsunami/forced evacuations killed 20,000 + people.
It’s data . . . and if it’s up for interpretation . . . it makes sense to know your audience. And I don’t think ‘depends on what you want to portray’ is an adequate defense. In this case, the stakes are really ginormous, but it makes sense to pay attention for everyday business data as well. Data in itself doesn’t take a POV – ethical or otherwise; so it is incumbent on the folks who present the data to be crystal clear about their intentions (which means being crystal clear about the data interpretations that do not support their POV).
Kudos to the authors.
Interesting results! There’s a similar survey experiment from Canada, where the authors find that logarithmic versus linear visualisations of COVID-19 cases do not affect citizens’ support for confinement. Maybe worth citing in your working paper? https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7200843/
EMH only works when there’s money involved?
I think the experiment shows that most people don’t like looking at the numbers on the axes; and that mixing up ordinary decimals and “so many k” makes this even worse. Both graphs are badly designed.
Thanks for the insight. I have a question regarding OLS regressions.
Is it preferable to use the log of COVID-19 deaths/infections for OLS or linear data?
To my knowledge logging data is used to tackle skewness and exponential growth which is not useful for linear regressions. But there are still studies who prefer to use level data on COVID-19 deaths/infections anyway. Could you give any statement on that?
Also, for my study I use log and level data which lead to different results and significance levels.
How to tackle this properly?
“Only 40.66% of them could respond correctly to a basic question about the [log scale] graph (whether there were more deaths in one week or another), contrasted to 83.79% of respondents on the linear scale. Moreover, people in the logarithmic group also proved to be worse at making predictions on the evolution of the pandemic: they predicted, on average, 71,250 deaths for a week after the experiment was taken, whereas the linear group predicted 63,429 (our ARIMA forecasting model indicated 55,791, and the actual number of deaths on that date was 54,256). ” Some questions are much easier to answer based on one graph than the other!!!!
It may be that eyesight, rather than just understanding, has a significant effect here. I presume the actual graphs seen by those taking part in the experiment were larger versions of the two graphs shown here, but even so… there are no fine grid lines to help read the data, and the question as to predicting the value for a week later involves extrapolating off the chart for the linear case. The errors in predictions (71,250 or 63,429 compared with 54,256 deaths for a week) may seem large numbers, and the answer for the logarithmic graph a long way off the correct (or even linear graph estimate), these answers are only wrong by a small fraction of an inch on those graphs. Being able to extrapolate (or even read data off the graph) with accuracy may be important in some situations, but it is a different skill to understanding overall trends.
Quite a lot has happened since the (May 2020 – almost 2 years ago!) experiment, and one frequently-seen device in online Covid graphs is the display of the exact numbers as the mouse hovers over data. This is very good, and obviously relates to the readability issue I mentioned. But a significant change is the desire by everyone to see whether the curve has (or is just about to) pass its peak. And meanwhile (I strongly expect) public appreciation of graphs and their significance has grown. And various ways of supplementing the graph’s information have been tried – other graphs alongside, or pointers to parts of the curve with data like (“123 deaths/day, doubling every 7.5 days”) – presumably in response to feedback.
So I hope there has been follow-up experiments like this, and it would be interesting to see graphed a measure of public understanding of graphical data during this pandemic – but should that graph be linear or logarithmic? 🙂