
 When you excessively screen job candidates, this could lower the expected average value of the accepted applicants, write Ehud Lehrer and David Lagziel.
When you excessively screen job candidates, this could lower the expected average value of the accepted applicants, write Ehud Lehrer and David Lagziel.
Screening occurs almost anywhere around us at any given moment. Though we might not be aware, it is essentially a daily routine. We screen career choices and investment opportunities; we screen job applicants, projects, and articles. Even the decision to read this blog post resulted from some form of screening, assuming that you do not read every blog post to ever be published on the internet.
So, what do we actually know of screening? This question stands at the core of our research agenda, whose first research paper is forthcoming. This paper is a theoretical one, which means that it is based on a mathematical problem, namely a decision problem, rather than on actual data. Yet, we do hope that empirical evidences will soon present themselves to support the subsequent reasoning.
Before we formally present the main result, let us first accurately define the problem using a well-known scenario from the business world. Assume that you are a manager who needs to recruit a few employees from a rather big set of applicants. Typically, to facilitate the process, you would probably define some threshold criteria that applicants need to meet in order to follow through to the next stage, or even get accepted. The idea to use threshold criteria is rather intuitive and for a good reason – in the absence of noise, which may distort the information regarding applicants, threshold criteria are an optimal screening strategy. This is a simple mathematical fact.
However, it appears that the introduction of a completely unbiased noise, that indeed distorts the manager’s available information, can actually lead to cases where threshold criteria perform rather poorly as screening strategies. In other words, once some noise enters the process, the optimal screening strategy needs to be adjusted accordingly.
This understanding leads to the phenomenon which we refer to as “a bias of screening”. In the absence of noise, there should be no biases with threshold screening. However, once non-trivial noises are introduced, it could be the case that a higher bar for screening would not only reduce the acceptance ratio, but could also lower the expected average value of the accepted applicants. In other words, a higher bar carries no quality assurances, as a lower one may produce a win-win situation on both sides of the quality versus quantity (alleged) trade-off.

To exemplify this result, we consider the following stylised theoretical example. As a manager, you receive a hundred applicant forms, CVs included, and you are able to derive some metric to evaluate the applicants on a standard 12-point grading scale, distributed as in Figure 1. Once you have the initial distribution you can decide whether to invite some of the applicants to a preliminary interview.
Figure 1 – The accurate evaluation

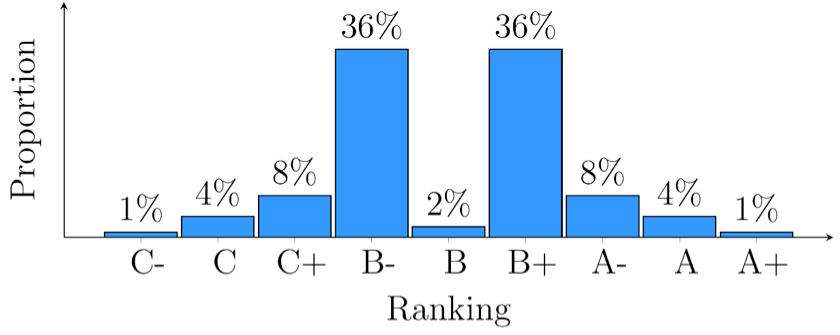
Now, the problem arises when either the forms, the CVs, or your metric do not accurately represent the true ranking. Thus enters the noise. Consider, for the sake of simplicity, that the original and accurate distribution is distorted by a noise such that each value remains unchanged with probability 0.8, whereas with probability 0.2 the valuation deviates by two levels, either upwards or downwards (symmetrically, each side with probability 0.1). Subject to this unbiased noise, you will probably see the distribution given in Figure 2, and the latter distribution is quite misleading.
Take, for example, the ‘A’ valuations. Clearly, these are not the true rankings, since the original and accurate distribution consists only of A-, B+, B-, and C+. The ‘A’ valuations were generated by the fact that a ranking of B+ that fluctuates by two levels either deviates upwards to A, or downwards to B-. Thus, if you were to set the bar at ‘A’ and above, you would interview mostly B+ applicants, while a bar at A- guarantees a majority of A- applicants. That is, a lower bar generates a higher average value!
Figure 2 – The noisy evaluation observed by the manager
The driving force behind this result, which extends well beyond this simplified example, is the influence of unbiased noise over different values. A mass of average elements, subject to unbiased noise, produces a relatively large number of (noisy) scores that pass a high threshold, while a similar effect over a small group of superior elements is relatively mild. To put it differently, the effect of unbiased noise is potentially biased by the action of screening.
This leads us to another conclusion of the paper, stating that such biases are more likely to occur at elite screening, rather than at low-level screening. The reason is that elite screening typically implies a low acceptance rate, which is easily affected by a small amount of sup-optimal elements that pass the screening due to the distorting noise.
In conclusion, this research provides a preliminary theoretical glance at the anomalies that may occur from screening processes. Though this is just the first step, we hope to induce more theoretical and empirical results, along with some constructive solutions to deal with the aforementioned concerns.
- This blog post appeared previously at LSE Business Review and is based on the authors’ paper “A Bias of Screening” in American Economic Review: Insights, forthcoming.
- Featured image by qimono, under a Pixabay licence
Please read our comments policy before commenting
Note: This article gives the views of the author, and not the position of USAPP– American Politics and Policy, nor of the London School of Economics.
Shortened URL for this post: http://bit.ly/2XF2uKK
About the authors
 Ehud Lehrer – Tel Aviv University
Ehud Lehrer – Tel Aviv University
Ehud Lehrer is a professor in the department of statistics and operations research at Tel Aviv University, Israel, and a research professor at INSEAD (Fontainebleau, France). He is an editor of the journal Games and Economic Behavior. His work deals with game theory, decision theory, economic theory and probability.
.
 David Lagziel – Ben-Gurion University of the Negev
David Lagziel – Ben-Gurion University of the Negev
David Lagziel is a tenure-track lecturer in the economics department at Ben-Gurion University of the Negev (Beer-Sheba, Israel). His work deals with game theory, economic theory, and labour economics.






